Satz des Euklid

Die Satzgruppe des Pythagoras, zu der der Satz des Euklid (Kathetensatz) gehört, zählt wegen ihrer großen Bedeutung für Berechnungen und Beweisführungen zu den berühmtesten der Planimetrie.

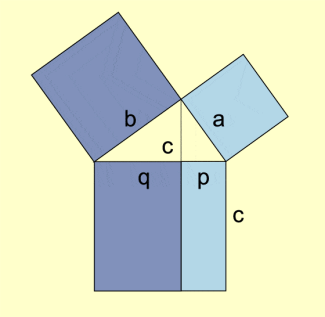
Satz des Euklid - der Kathetensatz

Im rechtwinkligen Dreieck ist das Quadrat über einer Kathete flächeninhaltsgleich dem Rechteck aus der Hypotenuse und dem zur Kathete gehörenden Hypotenusenabschnitt (Bild 1):
                       $a^2=c\cdot p{b}^2=c\cdot q$

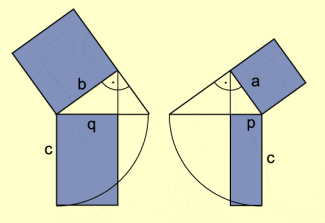
Beweis (über Ähnlichkeit)
Die Dreiecke ABC, CAH und BCH sind einander nach dem
Hauptähnlichkeitssatz ähnlich (Bild 2).
Es gilt: $\frac{a}{c}=\frac{p}{a}$, also $a^2=c\cdot p$ bzw. $\frac{b}{c}=\frac{q}{b}$, also $b^2=c\cdot q$

Der klassische Beweis des Satzes des Pythagoras benutzt den Kathetensatz, wobei die Anwendung des Satzes auf beide Katheten zum Satz des Pythagoras führt. Der Kathetensatz gibt auch die Möglichkeit, ein Quadrat in ein Rechteck, von dem eine Seitenlänge gegeben ist, zu verwandeln bzw. ein Rechteck in ein Quadrat.

Beispiel:
a) Verwandlung eines Dreiecks in ein flächeninhaltsgleiches Rechteck (Bild 3)
b) Verwandlung des Rechtecks in ein flächeninhaltsgleiches Quadrat (Bild 4)

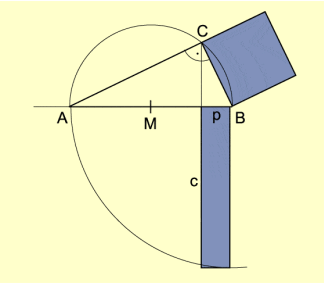
• Die kürzere Seite p des Rechtecks wird verlängert und von B aus die längere Seite c angetragen. Man erhält den Punkt A.
• AB wird halbiert und M ist der Mittelpunkt von AB.
• Über AB wird ein Halbkreis gezeichnet.
• Die längere Rechtecksseite c wird zum Schnitt mit dem Halbkreis verlängert, der Schnittpunkt ist C.

Nach Satz des Thales ist der Winkel bei C $90°$, das Dreieck ABC rechtwinklig. Das Quadrat über BC ist demnach flächeninhaltsgleich dem gegebenen Rechteck.

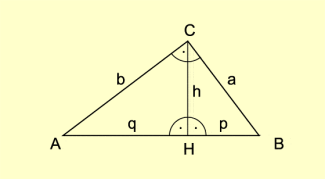
Umkehrung des Satzes des Euklid

Gelten für ein Dreieck mit den Seiten a, b und c, dessen Seite c durch die Höhe $h_c$ in die Abschnitte p und q geteilt wird, die Beziehungen $a^2=c\cdot p$ und $b^2=c\cdot q$, dann ist das Dreieck rechtwinklig (Bild 5).

Beweis erfolgt über den Satz des Pythagoras.