Verschiebung

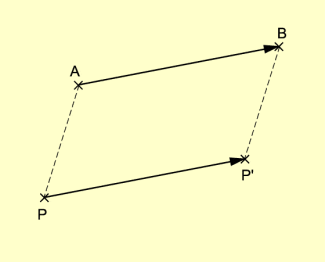
Eine Verschiebung $\overrightarrow{AB}$ (Parallelverschiebung, Translation) ist eine eineindeutige Abbildung der Ebene auf sich selbst, bei der für das Bild P' jedes Punktes P gilt:
$PP\text{'}\parallel AB$ und $AP\parallel BP\text{'}$ (Bild 1)

$\overrightarrow{AB}$ wird als Verschiebungspfeil bezeichnet. $\overrightarrow{PP}\text{'}$ hat stets die gleiche Länge und Richtung sowie den gleichen Richtungssinn wie $\overrightarrow{AB}$.

Jede Verschiebung ist mit der Angabe von Betrag, Richtung sowie Richtungssinn und damit durch den Verschiebungspfeil eindeutig gekennzeichnet. Neben den für jede Bewegung gültigen Eigenschaften gibt es spezielle Eigenschaften der Verschiebung:

• Jede zum Verschiebungspfeil parallele Gerade wird auf sich selbst abgebildet. Sie ist Fixgerade bei der Verschiebung.
• Die Verschiebung mit der Verschiebungsweite 0 ist die identische Abbildung.
• Bei keiner Verschiebung (außer der Identität) gibt es einen Fixpunkt.

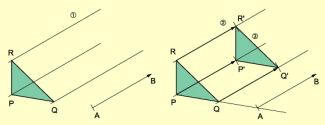
Konstruktion des Bildes eines Dreiecks bei einer Verschiebung

$\overrightarrow{AB}$ (Bild 2)

Konstruktionsbeschreibung:

1. Es werden Parallelen zu $\overrightarrow{AB}$ durch die Punkte P, Q und R gezeichnet.
2. Von R, P und Q aus wird jeweils auf der Parallelen die Länge der Strecke AB unter Beachtung der Orientierung abgetragen. Man erhält die Punkte R', P' und Q'.
3. Die Punkte R', P' und Q' werden miteinander verbunden.