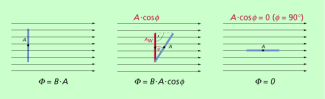Direkt zum Inhalt

Das Induktionsgesetz

Das Induktionsgesetz ist ein grundlegendes physikalisches Gesetz und die Grundlage für die Wirkungsweise solcher Geräte wie Transformatoren und Generatoren. In Worten kann man es so formulieren:
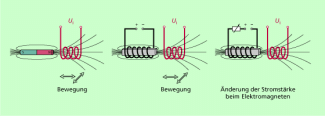
In einer Spule wird eine Spannung induziert, wenn sich das von der Spule umfasste Magnetfeld ändert. Der Betrag der Induktionsspannung ist umso größer, je schneller sich das von der Spule umfasste Magnetfeld ändert.
Eine allgemeine mathematische Formulierung des Induktionsgesetzes lautet:
U i = − N ⋅ d φ d t oder U i = − N ⋅ d ( B ⋅ A ) d t
Aus dieser allgemeinen Formulierung kann man alle wesentlichen Spezialfälle ableiten, insbesondere auch diejenigen, die der Wirkungsweise von Transformatoren und Generatoren zugrunde liegen.

Schule wird easy mit KI-Tutor Kim und Duden Learnattack

  • Kim hat in Deutsch, Mathe, Englisch und 6 weiteren Schulfächern immer eine von Lehrkräften geprüfte Erklärung, Video oder Übung parat.
  • 24/7 auf Learnattack.de und WhatsApp mit Bildupload und Sprachnachrichten verfügbar. Ideal, um bei den Hausaufgaben und beim Lernen von Fremdsprachen zu unterstützen.
  • Viel günstiger als andere Nachhilfe und schützt deine Daten.
Jetzt 30 Tage risikofrei testen

Diese Zusammenhänge kann man durch Grundversuche zur elektromagnetischen Induktion zeigen. Diese Grundversuche sind in einem gesonderten Beitrag auf der CD ausführlich erläutert.

Das Induktionsgesetz lässt sich aber auch in Form einer Gleichung für die Induktionsspannung darstellen und aus dieser allgemeinen Gleichung lassen sich die verschiedenen Spezialfälle ableiten. Dazu ist aber zunächst die Einführung einer weiteren physikalischen Größe erforderlich, die bei der mathematischen Formulierung des Induktionsgesetzes genutzt wird.

Der magnetische Fluss

Alle Experimente zur elektromagnetischen Induktion zeigen, dass der Betrag der Induktionsspannung abhängig ist

  • von der Änderung der Stärke des magnetischen Feldes, die man durch die magnetische Flussdichte B charakterisieren kann;
  • von der Fläche A der Spule, die sich im Magnetfeld befindet;
  • von der Windungszahl der Spule.

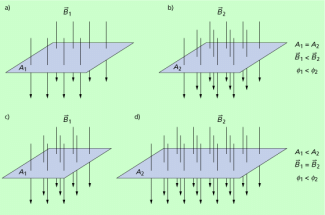
Wir betrachten zunächst die beiden zuerst genannten Punkte und eine Spule mit einer Windung, eine Leiterschleife der Fläche A. Dann kann man sich zunächst anschaulich mithilfe von Feldlinien darstellen, wie man ein Magnetfeld charakterisieren kann, das eine Fläche durchsetzt. Das Feld sei dabei senkrecht zur Fläche gerichtet (Bild 2). Die magnetische Flussdichte ist in dieser Darstellung ein Maß für die Dichte der Feldlinien. Sie ist also in Bild 2a, 2c und 2d gleich, in Bild 2b dagegen größer. Die Anzahl der Feldlinien als Maß für das Magnetfeld, das durch eine Fläche hindurchtritt, ist aber nicht nur von der Dichte der Feldlinien, sondern auch von der Größe der Fläche abhängig. Deshalb hat man als neue Größe den magnetischen Fluss eingeführt und definiert:

Ein magnetischer Fluss ist ein Maß für das die Fläche einer Leiterschleife durchsetzende Magnetfeld. Unter der Voraussetzung, dass die Fläche senkrecht zum Magnetfeld liegt, gilt für den magnetischen Fluss:
φ = B ⋅ A B magnetische Flussdichte A wirksame Fläche Die Einheit des magnetischen Flusses ist ein Weber (1 Wb): 1 Wb = 1   V ⋅ s
Benannt ist diese Einhe it nach dem Physiker WILHELM EDUARD WEBER (1804-1891), der in Göttingen eng mit CARL FRIEDRICH GAUSS zusammengearbeitet hat.

Als wirksame Fläche wird diejenige Fläche der Leiterschleife bezeichnet, die senkrecht vom magnetischen Feld durchsetzt wird (Bild 3). Aus den Skizzen ist erkennbar, dass sie bei einer gegebenen Leiterschleife zwischen der Fläche A dieser Leiterschleife und null betragen kann. Man kann also die wirksame Fläche beispielsweise durch Drehen einer Leiterschleife oder Spule im Magnetfeld zwischen dem Maximalwert A und null ändern.
Liegt eine Spule vor, dann kann man diese als aneinandergereihte Leiterschleifen auffassen. Beträgt die Windungszahl der Spule N, dann ist die maximale wirksame Fläche das N-fache einer Leiterschleife und es gilt allgemein für Spulen:

A g e s a m t = N ⋅ A ⋅ cos   ϕ N Windungszahl der Spule A Fläche einer Wicklung der Spule ϕ Winkel zwischen der Richtung des Magnetfeldes und der Flächennormalen

Eine allgemeine mathematische Formulierung des Induktionsgesetzes

Mithilfe der Größe magnetischer Fluss und der Feldgröße magnetische Flussdichte kann man das Induktionsgesetz in folgender allgemeinen Formulierung angeben:

U i = − N ⋅ d φ d t oder mit φ = B ⋅ A : U i = − N ⋅ d   ( B ⋅ A ) d t N Windungszahl φ magnetischer Fluss t Zeit B magnetische Flussdichte A wirksame Fläche
Das Minuszeichen ergibt sich aus energetischen Betrachtungen. Es hat keinen Einfluss auf den Betrag der Induktionsspannung.

Ableitung von Spezialfällen aus dem Induktionsgesetz

Wir gehen im Weiteren von dem Induktionsgesetz in der Form
U i = − N ⋅ d   ( B ⋅ A ) d t aus. Führt man die Differentiation aus, dann erhält man:
U i = − N ( A ⋅ d B d t + B ⋅ d A d t ) )

Daraus ergeben sich die folgenden Spezialfälle:

(1) Ist das Feld zeitlich konstant und damit, d B d t = 0 dann ergibt sich für die Induktionsspannung:
U i = − N ⋅ B ⋅ d A d t oder in Differenzenschreibweise U i = − N ⋅ B ⋅ Δ A Δ t

Das bedeutet: Im zeitlich konstanten Magnetfeld hängt die induzierte Spannung von der Änderungsgeschwindigkeit der wirksamen Fläche ab. Genutzt wird dieser Zusammenhang bei Generatoren. Genauere Hinweise zu deren Aufbau und Wirkungsweise sind unter dem Stichwort „Generatoren“ zu finden.

(2) Die Leiterschleife oder Spule ruht in einem veränderlichen Magnetfeld. Damit ist d A d t = 0 und für die Induktionsspannung ergibt sich:
U i = N ⋅ A ⋅ d B d t oder in Differenzenschreibweise U i = N ⋅ A ⋅ Δ B Δ t

Das bedeutet: Im zeitlich veränderlichen Magnetfeld hängt die dort in einer ruhenden Spule induzierte Spannung von der Änderungsgeschwindigkeit der magnetischen Flussdichte ab. Genutzt wird dieser Zusammenhang bei Transformatoren. Genauere Hinweise zu deren Aufbau und Wirkungsweise sind unter dem Stichwort „Transformatoren“ zu finden.

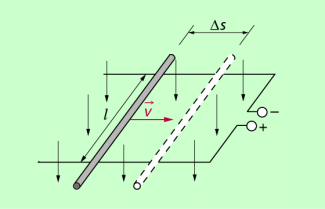
(3) Auch die Spannung zwischen den Enden eines Leiters kann man aus dem Induktionsgesetz ableiten. Dazu betrachten wir den in Bild 4 dargestellten Sachverhalt: Ein Leiter der Länge l wird in einem dazu senkrechten, zeitlich konstanten Magnetfeld bewegt. Für diesen Fall könnte man das Induktionsgesetz in folgender Form anwenden:
U i = − B ⋅ Δ A Δ t Mit Δ A = l ⋅ Δ s erhält man: U i = − B ⋅ l ⋅ Δ s Δ t Nun ist , eine gleichförmige Bewegung vorausgesetzt , Δ s Δ t = v . Damit erhält man: U i = − B ⋅ l ⋅ v B magnetische Flussdichte l Länge des Leiters v Geschwindigkeit des Leiters

Die gleiche Beziehung kann man auch durch Anwendung der LORENTZ-Kraft oder durch energetische Betrachtungen gewinnen.

Wendet man die LORENTZ-Kraft auf einen Leiter mit frei beweglichen Elektronen an, der sich senkrecht zu den Feldlinien bewegt, dann gilt:
F L = − e ⋅ v ⋅ B
Die Ladungsverschiebung infolge des Wirkens der LORENTZ-Kraft geht solange vor sich, bis die dadurch entstehende Feldkraft genauso groß ist wie die LORENTZ-Kraft. Es gilt dann also:
F Feld = F L Setzt man für die LORENTZ-Kraft den Term − e ⋅ v ⋅ B ein , so erhält man: F Feld = − e ⋅ v ⋅ B oder F Feld e = − v ⋅ B (1) Nimmt man im Leiter ein homogenes Feld an , dann ist F Feld e = E = U l . Einsetzt in Gleichung (1) ergibt sich: U l = − v ⋅ B oder U = U i = − l ⋅ v ⋅ B
Mit energetischen Betrachtungen kann man folgendermaßen herangehen:
Bei der elektromagnetischen Induktion wird mechanische Energie in elektrische Energie umgewandelt. Um den Leiter zu bewegen, ist eine Kraft erforderlich. Es muss die mechanische Arbeit W mech = F ⋅ Δ s verrichtet werden. Es entsteht die elektrische Energie E e l = U ⋅ I ⋅ Δ t .
Im Idealfall ist nach dem Energieerhaltungssatz die entstehende elektrische Energie genauso groß wie die verrichtete mechanische Arbeit. Es gilt also:
F ⋅ Δ   s = U ⋅ I ⋅ Δ   t Der entstehende Induktionstrom ruft eine Feldkraft hervor , die der Kraft F entgegengerichtet ist und den Betrag l ⋅ l ⋅ B hat . Damit ergibt sich: − l ⋅ l ⋅ B ⋅ Δ   s = U ⋅ I ⋅ Δ   t oder vereinfacht: − l ⋅ B ⋅ Δ   s = U ⋅ Δ   t Durch Umstellung nach U erhält man: U = − l ⋅ B ⋅ Δ   s Δ   t und mit Δ   s Δ   t = v : U = − l ⋅ B ⋅ v

Lernhelfer (Duden Learnattack GmbH): "Das Induktionsgesetz." In: Lernhelfer (Duden Learnattack GmbH). URL: http://www.lernhelfer.de/index.php/schuelerlexikon/physik-abitur/artikel/das-induktionsgesetz (Abgerufen: 19. May 2025, 20:56 UTC)

Suche nach passenden Schlagwörtern