Elektrisches Potenzial und elektrische Spannung

Ähnlich wie beim Gravitationsfeld wird auch beim elektrischen Feld ein Potenzial definiert. Unter dem elektrischen Potenzial eines Punktes versteht man den Quotienten aus der potenziellen Energie in diesem Punkt und der Ladung des Körpers. Allgemein wird das elektrische Potenzial folgendermaßen definiert:
$\begin{array}{l}\varphi =\frac{E_{\text{pot}}}{Q_{\text{P}}}={\displaystyle \underset{r_0}{\overset{r_1}{\int }}\overrightarrow{E}(r)\text{d}\overrightarrow{r}}\\ E_{\text{pot}}\text{potenzielle Energie}\\ Q_{\text{P}}\text{Ladung der Probeladung im Feld}\\ E\text{elektrische Feldstärke}\\ r{\text{Weg zwischen den Punkten P}}_{\text{0}}{\text{und P}}_{\text{1}}\end{array}$

Dabei ist es üblich, einem (willkürlich gewählten) Punkt ${\text{P}}_{\text{0}}$ das Potenzial null zuzuordnen. Um Missverständnisse zu vermeiden, sollte das gewählte Nullpotenzial stets mit angegeben werden. Statt der Bezeichnung r für den Abstand nutzt man auch die Bezeichnung s für den Weg.
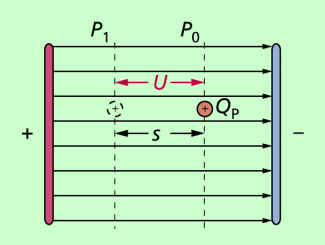
In einem homogenen elektrischen Feld (Bild 1) wählen wir einen beliebigen Punkt ${\text{P}}_{\text{0}}$ als Nullpotenzial, ordnen ihm also den Wert null zu. Das Potenzial in einem beliebigen anderen Punkt ${\text{P}}_{\text{1}}$ beträgt dann:
$\begin{array}{l}\varphi =\frac{Q_P\cdot E\cdot s}{Q_P}=E\cdot s\\ E\text{elektrische Feldstärke}\\ s\text{Weg im homogenen Feld}\end{array}$

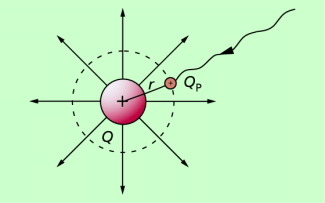
In einem Radialfeld wählt man als Bezugspunkt für das Nullpotenzial meist einen Punkt im Unendlichen. Dann ergibt sich für das Potenzial in der Entfernung r von der felderzeugenden Ladung:
$\begin{array}{l}\varphi ={\displaystyle \underset{\infty }{\overset{r}{\int }}E(r)\text{d}r}\\ \text{Setzt man für die Feldstärke des Radialfeldes}\\ E(r)=\frac{1}{4\pi \cdot {\epsilon }_0\cdot {\epsilon }_r}\cdot \frac{Q}{r^2},\text{so erhält man:}\\ \varphi ={\displaystyle \underset{\infty }{\overset{r}{\int }}\frac{1}{4\pi \cdot {\epsilon }_0\cdot {\epsilon }_r}\cdot \frac{Q}{r^2}\text{d}r}\text{oder}\\ \varphi =\frac{Q}{4\pi \cdot {\epsilon }_0\cdot {\epsilon }_r}\cdot {\displaystyle \underset{\infty }{\overset{r}{\int }}\frac{1}{r^2}}\text{d}r\\ \text{Integration und Einsetzen der Grenzen ergibt:}\\ \varphi =\frac{1}{4\pi \cdot {\epsilon }_0\cdot {\epsilon }_r}\cdot \frac{Q}{r}\end{array}$

Elektrisches Potenzial und elektrische Spannung

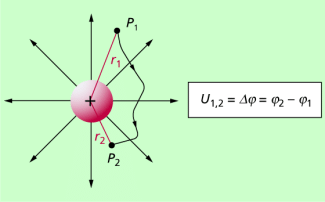
Aus den Gleichungen für das Potenzial ist ableitbar: Das Potenzial bezieht sich immer auf einen bestimmten Punkt im elektrischen Feld einer felderzeugenden Ladung. Die Potenzialdifferenz zwischen zwei Punkten ist gleich der elektrischen Spannung zwischen diesen Punkten:
$U=\Delta \varphi ={\varphi }_2-{\varphi }_1$
Der Betrag der Potenzialdifferenz und damit auch der Spannung ist unabhängig davon, welcher Punkt als Nullpotenzial gewählt wurde.

Feldlinien und Äquipotenziallinien

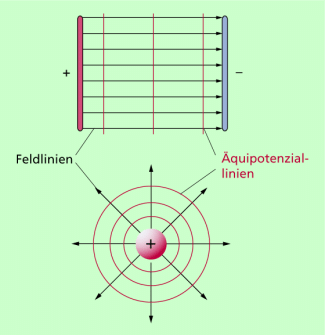
Ein elektrisches Feld kann man mithilfe des Modells Feldlinienbild beschreiben. Der Abstand der Feldlinien ist ein (relatives) Maß für die Stärke des elektrischen Feldes.
Eine andere Möglichkeit ist die grafische Veranschaulichung von Feldern mit Äquipotenziallien in der Ebene oder Äquipotenzialflächen im Raum. Eine Äquipotenziallinie bzw. Äquipotenzialfläche ist eine Linie bzw. eine Fläche, die Orte gleichen Potenzials verbindet.
Daraus ergibt sich: Feldlinien und Äquipotenziallinien stehen senkrecht aufeinander (Bild 4).