Freier Fall

Der freie Fall - eine Bewegung mit konstanter Beschleunigung

Für den freien Fall gelten die Gesetze der gleichmäßig beschleunigten Bewegung. Die Beschleunigung, mit der ein frei fallender Körper fällt, wird als Fallbeschleunigung g bezeichnet. Da die Fallbeschleunigung vom jeweiligen Ort abhängig ist, nennt man sie manchmal auch Ortsfaktor, bezogen auf die Erde auch Erdbeschleunigung. Die Fallbeschleunigung an der Erdoberfläche hat folgende Werte:

$\begin{array}{l}\text{am Äquator: 9}\text{,787 m}\cdot {\text{s}}^{-2}\\ \text{am Pol: 9}\text{,832 m}\cdot {\text{s}}^{-2}\\ \text{mittlerer Wert: 9}\text{,806}65\text{m}\cdot {\text{s}}^{-2}\\ \text{Häufig wird mit dem Näherungswert}\\ g=10\text{m}\cdot {\text{s}}^{-2}\text{gerechnet}\text{.}\end{array}$

Weit oberhalb der Erdoberfläche oder auf anderen Himmelskörpern hat die Fallbeschleunigung andere Werte, z.B:

$\begin{array}{l}\text{in 10}\text{km Höhe über der Erdoberfläche: 9}\text{,78 m}\cdot {\text{s}}^{-2}\\ \text{in 100 km Höhe über der Erdoberfläche: 9}\text{,52 m}\cdot {\text{s}}^{-2}\\ \text{in 1000 km Höhe über der Erdoberfläche: 7}\text{,33 m}\cdot {\text{s}}^{-2}\end{array}$

Die Hälfte ihres Wertes auf der Erdoberfläche erreicht die Fallbeschleunigung erst in einer Höhe von 2460 km. Die Fallbeschleunigung auf der Erdoberfläche kann in unterschiedlicher Weise bestimmt werden. Genauere Informationen dazu sind unter dem Stichwort „Fallbeschleunigung“ zu finden
Werte für g auf der Oberfläche anderer Himmelskörper sind:

$\begin{array}{l}\text{Mond: 1}\text{,62 m}\cdot {\text{s}}^{-2}\\ \text{Mars: 3}\text{,71 m}\cdot {\text{s}}^{-2}\\ \text{Venus: 8}\text{,87 m}\cdot {\text{s}}^{-2}\\ \text{Jupiter: 24}\text{,88 m}\cdot {\text{s}}^{-2}\\ \text{Sonne: 274 m}\cdot {\text{s}}^{-2}\end{array}$

Gesetze des freien Falles

Die Gesetze des freien Falls wurden von GALILEO GALILEI (1564-1642) gefunden. Die Entdeckung der Fallgesetze ist in einem gesonderten Beitrag dargestellt.
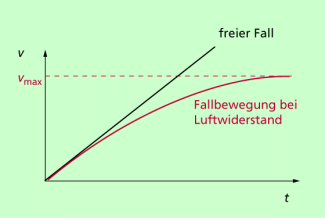
Die Fallgesetze gelten nur im Vakuum, also bei einer Bewegung ohne Luftwiderstand. Nur im Vakuum fallen alle Körper gleich schnell. Die Gesetze gelten auch näherungsweise für den Fall in Luft, wenn der Luftwiderstand vernachlässigt werden kann. Das kann bei schweren Körpern und kleinen Fallstrecken bzw. kleinen Fallzeiten angenommen werden.
Für den freien Fall gelten das Weg-Zeit-Gesetz und Geschwindigkeit-Zeit-Gesetz:

$\begin{array}{l}\text{Weg-Zeit-Gesetz:}s=\frac{a}{2}{t}^2\\ \text{Geschwindigkeit-Zeit-Gesetz:}v=a\cdot t\\ s\text{Weg}\\ v\text{Geschwindigkeit}\\ a\text{Beschleunigung}\\ t\text{Zeit}\end{array}$
Durch Kombination dieser beiden Gesetze lassen sich weitere Zusammenhänge formulieren. Stellt man das Geschwindigkeit-Zeit-Gesetz nach der Zeit t um und setzt den Term in das Weg-Zeit-Gesetz ein, so erhält man:

$\begin{array}{l}s=\frac{v^2}{2g}\\ \text{Die Umstellung nach}v\text{ergibt:}v=\sqrt{2g\cdot s}\\ \text{Die Umstellung nach}g\text{ergibt:}g=\frac{v^2}{2s}\end{array}$

Häufig ersetzt man auch den Weg s durch die Höhe h und erhält dann die Gleichungen:

$s=\frac{v^2}{2h}v=\sqrt{2g\cdot h}g=\frac{v^2}{2h}$

Grenzen der Anwendbarkeit der Gesetze

Der Fall eines Steines aus 20 m Höhe oder der Sprung einer Person von einem 10-m-Turm können als freier Fall betrachtet werden, da in diesen Fällen der Luftwiderstand vernachlässigt werden kann. Für einen am Fallschirm schwebenden Fallschirmspringer sind die Gesetze des freien Falls nicht anwendbar, weil in diesem Fall der Luftwiderstand nicht vernachlässigt werden kann. Auch für Regentropfen gelten die Gesetze des freien Falls nicht. So erreichen aufgrund des Luftwiderstandes

• ohne geöffneten Fallschirm aus großer Höhe fallende Menschen eine Geschwindigkeit von etwa 200 km/h,
• Regentropfen in unmittelbarer Nähe des Erdbodens je nach Größe eine Geschwindigkeit von bis zu 30 km/h.

Will man bei der Lösung von Aufgaben die Gesetze des freien Falls anwenden, so muss man stets prüfen, ob der Luftwiderstand beim gegebenen Sachverhalt vernachlässigbar ist.

Untersuchungen bei frei fallenden Körpern

Fällt ein Körper frei, so wirkt auf ihn keine Gewichtskraft. Er ist schwerelos. Es ist von erheblichem wissenschaftlichen Interesse zu untersuchen, wie sich verschiedene Körper unter diesen Bedingungen verhalten. Solche Untersuchungen kann man im Weltraum realisieren. Sie sind aber auch der Erde durchführbar, wenn auch nur in kurzen Zeitintervallen. Eine Anordnung, mit der man solche Untersuchungen durchführen kann, ist der Fallturm in Bremen. Genauere Informationen sind unter dem Stichwort „Fallturm“ zu finden.