Interferenz von Licht

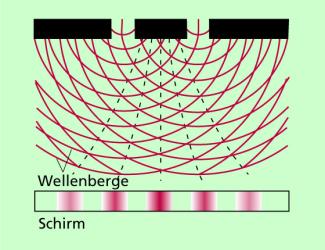
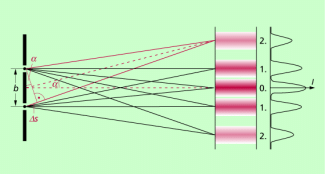
Lenkt man Licht, das von einer Lichtquelle kommt, auf einen schmalen Doppelspalt, dann kann man in einem gut abgedunkelten Raum auf einem Schirm hinter dem Doppelspalt eine Reihe von hellen und dunklen Streifen beobachten (Bild 1). Diese Interferenzstreifen sind Ausdruck dafür, dass sich das von den beiden Spalten ausgehende Licht überlagert (interferiert).

Unter der Interferenz von Licht versteht man die Erscheinung, dass sich das von einer Lichtquelle ausgehende Licht überlagert und damit Bereiche der Verstärkung und Abschwächung oder Auslöschung auftreten.

Eine solche Interferenz von Licht erfolgt ständig, stabile Interferenzmuster sind aber nur unter bestimmten Bedingungen zu beobachten.

Bedingungen für stabile Interferenzmuster

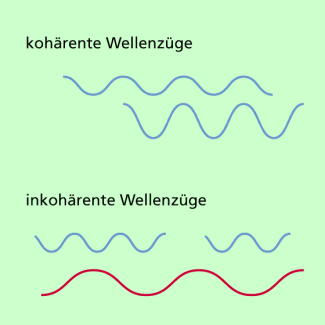
Das Licht einer Lichtquelle entsteht durch atomare Prozesse in der Atomhülle. Geht man vom Wellenmodell aus, dann gilt: Bei den meisten Lichtquellen sind die Lichtwellenzüge, die von der Lichtquelle ausgehen, im Raum unterschiedlich orientiert. Es kommt damit zwar zu Überlagerungen, nicht aber zu einem stabilen Interferenzmuster. Ein solches stabiles Interferenzmuster entsteht nur dann, wenn die betreffenden Lichtwellen bei gleicher Frequenz bzw. Wellenlänge eine feste Phasenbeziehung zueinander haben. Solche Wellen nennt man kohärent. Ist die Bedingung nicht erfüllt, so spricht man von inkohärentem Licht. Das Licht aller natürlichen Lichtquellen ist inkohärent (Bild 2).
Kohärente Wellen oder kohärentes Licht erhält man, indem man das Licht einer Lichtquelle durch geeignete Anordnungen (Spalte, Gitter, Prismen, Spiegel) zunächst aufteilt und diese Teile dann wieder zur Überlagerung bringt. Damit wird genutzt, dass das Licht, das von einem Punkt einer Lichtquelle ausgeht, mit sich selbst kohärent ist.

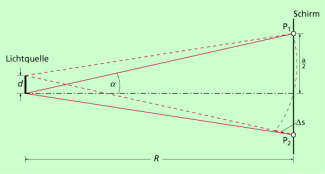
Dabei wird mitunter eine Bedingung angegeben, die man als Kohärenzbedingung bezeichnet. Sie ergibt sich aus folgender Überlegung (Bild 3): Liegt eine ausgedehnte Lichtquelle vor, dann ist das von einem Punkt dieser Lichtquelle ausgehende Licht mit sich selbst kohärent. Zwei vom gleichen Punkt in der Mitte ausgehende sehr schmalen Lichtbündel (rote Linien) haben auf dem Schirm in den Punkten 1 und 2 den optischen Gangunterschied null. Die vom oberen Rand der Lichtquelle ausgehenden (gestrichelt gezeichneten) Lichtbündel haben in den Punkten 1 und 2 den Gangunterschied:
$\begin{array}{l}\Delta x=\frac{a\cdot d}{R}\\ \text{Die von der Mitte und vom Rand der Lichtquelle}\\ \text{stammende Wellen sind fast gleichphasig}\text{, wenn}\\ \Delta x\ll \frac{\lambda }{2}\text{ist}\text{. Damit erhält man:}\\ \frac{a\cdot d}{R}\ll \frac{\lambda }{2}\\ \text{oder mit}\frac{a}{2r}=\tan \alpha \\ 2d\cdot \tan \alpha \ll \frac{\lambda }{2}\end{array}$
Die zuletzt genannte Beziehung ist die Kohärenzbedingung. Dabei ist d der Abstand zweier Punkte einer Lichtquelle.
Eine andere Möglichkeit ist die Verwendung kohärenter Lichtquellen. So senden beispielsweise Laser kohärentes Licht aus. Deshalb lässt sich auch mithilfe von Lasern die Interferenz besonders einfach demonstrieren.

Bedingungen für Verstärkung und Auslöschung

Wenn sich kohärentes Licht überlagert, kommt es je nach dem Gangunterschied zwischen den zwischen den interferierenden Wellen zu einer Verstärkung, Abschwächung oder Auslöschung.
Beträgt der Gangunterschied null, die Wellenlänge $\lambda$ oder ein ganzzahliges Vielfaches davon, so erfolgt eine maximale Verstärkung. Es ist dann ein Schwingungsbauch vorhanden, die betreffende Stelle ist hell. Man bezeichnet das auch als konstruktive Interferenz. Für sie gilt die Bedingung:
$\Delta s=k\cdot \lambda \text{(}k=\mathrm{0,}\pm \mathrm{1,}\pm \mathrm{2,}\mathrm{...})$
Abschwächung ist vorhanden, wenn diese Bedingung nicht erfüllt ist. Beträgt der Gangunterschied gerade eine halbe Wellenlänge oder ein ungeradzahliges Vielfaches davon, dann tritt Auslöschung auf. Es ist dann an der betreffenden Stelle ein Schwingungsknoten vorhanden, die Stelle ist dunkel. Man bezeichnet das auch als destruktive Interferenz. Für sie gilt die Bedingung:
$\Delta s=k\cdot \frac{\lambda }{2}\text{(}k=\pm \mathrm{1,}\pm \mathrm{3,}\pm \mathrm{5,}\mathrm{...})$
Bringt man z.B. hinter einem Doppelspalt einen Schirm an, dann zeigt sich ein Wechsel von hellen und dunklen Streifen. Die hellen Streifen haben bei Verwendung von einfarbigem (monochromatischem) Licht die Farbe dieses Lichtes. Bei Verwendung von weißem Licht sieht man außer im Maximum 0. Ordnung ein kontinuierliches Spektrum, weil die Lage der Maxima wellenlängenabhängig ist.

Interferenz am Einzelspalt

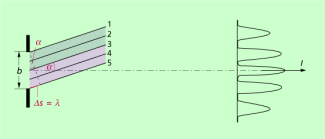
Bei einem Einzelspalt ist nach dem huygensschen Prinzip jeder Punkt dieses Spaltes Ausgangspunkt für Elementarwellen, die sich überlagern (Bild 4). Ist der Gangunterschied zwischen den beiden Randstrahlen gleich einer Wellenlänge, dann kann man zu jedem Strahl aus der einen Hälfte des Lichtbündels einen Strahl aus der anderen Hälfte finden, zwischen denen der Gangunterschied gerade die halbe Wellenlänge beträgt (Bild 4). Beispiele dafür sind die Strahlen 1 und 3 oder 2 und 4. Es kommt folglich zu Auslöschung aller Wellen. Vergrößert sich der Gangunterschied, dann kommt es zu einer partiellen Auslöschung. Das restliche Licht bildet ein Maximum 1. Ordnung. Es entstehen helle und dunkle Streifen. Für die Minima gilt die Bedingung:
$\begin{array}{l}\sin {\alpha }_k=\frac{k\cdot \lambda }{b}k=(\pm \mathrm{1,}\pm \mathrm{2,}\mathrm{..}.\\ \lambda \text{Wellenlänge}\\ b\text{Spaltbreite}\end{array}$
Die Bedingung für Maxima lautet:
$\sin {\alpha }_k=\frac{(2k+1)\lambda }{2b}(k=\pm \mathrm{1,}\pm \mathrm{2,}\mathrm{...})$

Interferenz am Doppelspalt

Bild 5 zeigt ein typisches Interferenzmuster, das man durch einen Doppelspalt erhält. Es treten neben dem Maximum 0. Ordnung weitere ausgeprägte Maxima und Minima auf. Ihre Lage kann man relativ einfach ermitteln.

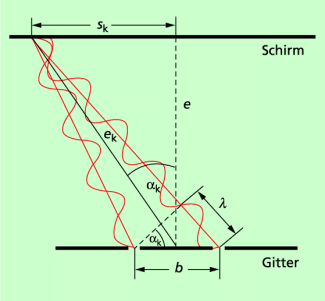
Wir betrachten dazu den in Bild 6 dargestellten Fall. Allgemein gilt: Wie bei mechanischen Wellen tritt eine Verstärkung dann auf, wenn bei gleicher Wellenlänge und fester Verschiebung zwischen zwei Wellenzügen sich jeweils Wellenberge bzw. Wellentäler überlagern. Das ist dann der Fall, wenn der Gangunterschied zwischen zwei Wellenzügen null, eine Wellenlänge oder ein Vielfaches davon beträgt, also konstruktive Interferenz vorliegt. Für die Maxima gilt dann die Bedingung:
$\begin{array}{l}\sin {\alpha }_k=\frac{k\cdot \lambda }{b}\text{(}k=\mathrm{0,}\pm \mathrm{1,}\pm \mathrm{2,}\mathrm{...})\\ \lambda \text{Wellenlänge}\\ b\text{Abstand der beiden Spalte}\end{array}$

Der Winkel lässt sich unter der Voraussetzung, dass der Spaltabstand klein gegenüber der Entfernung Doppelspalt-Schirm ist, aus durch folgende Beziehung ausdrücken:
$\sin {\alpha }_k=\frac{s_k}{e}$
Damit kann man auch schreiben:
$\frac{k\cdot \lambda }{b}=\frac{s_k}{e}\text{(unter der Bedingung}{s}_k\ll e)$
Diese Beziehung kann man nutzen, um die Wellenlänge von Licht zu bestimmen. Dafür nutzt man aber zweckmäßigerweise keinen Doppelspalt, sondern ein optisches Gitter.

Interferenz am Gitter

Das auf ein optisches Gitter fallende Licht wird wie beim Doppelspalt (Bild 5) an jedem einzelnen Spalt gebeugt, d. h. es breitet sich nach dem betreffenden Spalt in den unterschiedlichsten Richtungen aus. Damit überlagert sich hinter dem Gitter das von den einzelnen Spalten ausgehende Licht. Es kommt in bestimmten Bereichen zur Verstärkung bzw. zur Abschwächung oder Auslöschung. Bringt man hinter dem Gitter einen Schirm an, so kann man auf ihm typische Interferenzstreifen, also helle und dunkle Linien, beobachten. Dabei zeigt sich: Mit Erhöhung der Anzahl der Spalte prägen sich die Maxima immer schärfer aus. Nur sie sind auch für Messungen von Interesse. Wie beim Doppelspalt gilt auch beim Gitter für die Maxima:
$\begin{array}{l}\sin {\alpha }_k=\frac{k\cdot \lambda }{b}\text{(}k=\mathrm{0,}\pm \mathrm{1,}\pm \mathrm{2,}\mathrm{...})\\ \lambda \text{Wellenlänge}\\ b\text{Gitterkonstante}\end{array}$

Optische Gitter

Ein Gitter wird hergestellt, indem man in eine Glasplatte oder in eine spiegelnde Metallplatte mit einem Diamanten in gleichen Abständen feine Furchen einritzt. Die nicht geritzten Teile wirken wie sehr schmale Spalte.
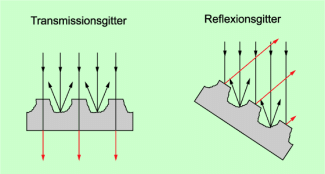
Nutzt man Glas, so geht das Licht durch die nicht geritzten Teile hindurch. Eine solche Art von Gitter bezeichnet man auch als Transmissionsgitter.
Bei einer spiegelnden Metallfläche geht dagegen dass Licht nicht hindurch, sondern wird an den nicht geritzten Stellen reflektiert. Eine solche Art von Gitter bezeichnet man deshalb als Reflexionsgitter.
Transmissionsgitter lassen sich auch relativ einfach auf fotografischem Wege herstellen: Zeichnet man auf ein Blatt Papier parallele schwarze Linien und fotografiert diese, so kann das Negativ als optisches Gitter verwendet werden.
Erfunden wurde das Gitter durch den deutschen Physiker JOSEPH VON FRAUNHOFER (1787-1826). FRAUNHOFER stellte mit einer speziell entwickelten Ritzmaschine Gitter mit einer Gitterkonstanten von bis zu 3.31 Mikrometer her. Er nutzte dazu Glasplatten, in die feine Furchen eingeritzt wurden, und erhielt damit Transmissionsgitter.
Der amerikanische Physiker HENRY AUGUSTUS ROWLAND (1848-1901) ritzte Spiegelmetall. Ihm gelang es, 20 000 Linien auf ein englisches Zoll zu ritzen. Das so entstandene Reflexionsgitter hatte eine Gitterkonstante von 1,27 Mikrometer. Solche Reflexionsgitter werden nach ihrem Erfinder auch als ROWLAND-Gitter bezeichnet.

Interferenz durch Brechung und Reflexion

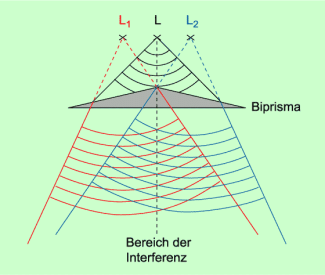
Versuche mit einem Doppelspalt, die auf den englischen Mediziner und Physiker THOMAS YOUNG (1773-1829) zurückgehen, waren die historisch ersten Experimente zur Untersuchung der Interferenz bei Licht. Weitere Experimentieranordnungen zur Interferenz von Licht entwickelten der französische Physiker AUGUSTIN JEAN FRESNEL (1788-1826) sowie der deutsche Naturforscher JOSEPH VON FRAUNHOFER (1787-1826) mit der Erfindung des optischen Gitters. Allen diesen Experimentieranordnungen ist gemeinsam, dass Licht einer Lichtquelle geteilt wird und diese Teile zur Überlagerung gebracht werden. Bei dem von FRESNEL vorgeschlagenen Biprisma (Bild 9) wird das von einer Lichtquelle L ausgehende Licht gebrochen. Die Teile überlagern sich hinter dem Biprisma. Es entsteht ein Interferenzbild. Das Licht scheint infolge der Brechung von zwei Lichtquellen herzukommen.

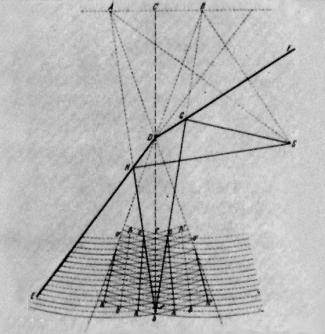
Interferenz lässt sich auch durch Reflexion hervorrufen. Bild 10 zeigt eine Anordnung mit einem Winkelspiegel, so wie sie von FRESNEL vorgeschlagen wurde. Das Bild zeigt eine eigenhändige Zeichnung von FRESNEL. Das Licht geht von einer Lichtquelle S aus und trifft auf einen Winkelspiegel (FRESNEL-Spiegel), dessen Flächen nur geringfügig gegeneinander geneigt sind. Das an den beiden Flächen reflektierte Licht überlagert sich. Die Anordnung wirkt dabei so, als ob das Licht von den beiden (fiktiven) Lichtquellen A und B herzukommen scheint.