LORENTZ-Transformation

Zur historischen Einordnung

Sein Anliegen war, die Versuchsergebnisse von MICHELSON und MORLEY im Rahmen der klassischen Physik widerspruchsfrei zu deuten. Dazu entwickelte er 1895 Gleichungen, die es ermöglichten, die räumlichen und zeitlichen Koordinaten von einem Inertialsystem in ein anderes umzurechnen.
LORENTZ blieb dabei in den klassischen Vorstellungen des absoluten Raumes mit einem ruhenden Äther verhaftet und ging nicht von der Konstanz der Lichtgeschwindigkeit, sondern davon aus, dass sich bei Bewegung eines Körpers dessen Länge verringert (LORENTZ-Kontraktion).
ALBERT EINSTEIN formulierte 10 Jahre später als eines seiner zwei Ausgangspostulate das Postulat von der Konstanz der Lichtgeschwindigkeit. Die von LORENTZ angegebenen Gleichungen erwiesen sich als richtig, erfuhren aber durch EINSTEIN eine völlig neue, relativistische Deutung. Es ist somit EINSTEINs Verdienst, die grundsätzliche Bedeutung der in den Formeln enthaltenen Zusammenhänge erkannt zu haben.

Das Wesen der LORENTZ-Transformation aus relativistischer Sicht

Für die Beschreibung von Ereignissen in unterschiedlichen Inertialsystemen wird in der klassischen Physik, also bei kleinen Relativgeschwindigkeiten, die GALILEI-Transformation genutzt. Für große Geschwindigkeiten ist die GALILEI-Transformation nicht mehr anwendbar.

Die Gleichungen, die es ermöglichen, die räumlichen und zeitlichen Koordinaten von einem Inertialsystem in ein anderes umzurechnen, das sich mit beliebiger Geschwindigkeit dazu bewegt, werden als LORENTZ-Transformationsgleichungen bezeichnet.

Wir gehen nachfolgend von folgenden Bedingungen aus:

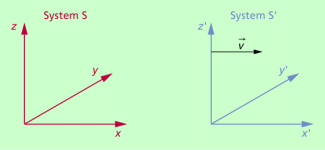
• Betrachtet werden zwei Inertialsysteme S und S' (Bild 2). Das System S' bewegt sich gegenüber dem System S mit der Geschwindigkeit v in positiver x-Richtung.
• Zum Zeitpunkt t = t' = 0 ist auch x = x' = 0. Die Ursprünge der beiden Koordinatensysteme fallen also zur Zeit t = t' = 0 zusammen.
• Zur verkürzten Formulierung der Gleichungen nutzen wir den LORENTZ-Faktor (k-Faktor, Bewegungsfaktor, relativistischer Faktor):

$k=\frac{1}{\sqrt{1-v^2/c^2}}$

Dabei ist v die Relativgeschwindigkeit der beiden Systeme S und S' zueinander und c die Vakuumlichtgeschwindigkeit.
Dann gelten die folgenden Transformationsgleichungen:

Für kleine Geschwindigkeiten weit unterhalb der Vakuumlichtgeschwindigkeit geht der Faktor
$v^2/c^2\text{bzw}.v/c^2$
gegen null. Damit geht für kleine Geschwindigkeiten die LORENTZ-Transformation in die klassische GALILEI-Transformation über.
Erfolgt die Bewegung der Systeme S und S' zueinander nicht in x-Richtung, so müssen die Transformationsgleichungen den jeweiligen Bedingungen angepasst werden.

Ab welchen Geschwindigkeiten man die LORENTZ-Transformation nutzen muss, hängt von der geforderten Genauigkeit ab. Eine Aussage darüber lässt sich aus dem LORENTZ-Faktor ableiten. Nachfolgend sind deshalb einige Werte für diesen Faktor
$k=\frac{1}{\sqrt{1-v^2/c^2}}$
bei unterschiedlichen Geschwindigkeiten v angegeben.

Aus dieser Übersicht ist erkennbar, dass bei den Geschwindigkeiten, die im Alltag eine Rolle spielen, der k-Faktor vernachlässigbar klein ist und demzufolge auch die LORENTZ-Transformation für diesen Bereich keine Bedeutung hat. Anders ist das bei schnell bewegten Elektronen oder bei anderen Elementarteilchen, die sich durchaus mit über 90 % der Lichtgeschwindigkeit bewegen können.

Herleitung der LORENTZ-Transformation

Die Transformationsgleichungen können in unterschiedlicher Weise hergeleitet werden. Nachfolgend ist eine Möglichkeit der Herleitung dargestellt.
Ausgangspunkt ist das Prinzip von der Konstanz der Lichtgeschwindigkeit. Darüber hinaus muss in den Transformationsgleichungen die GALILEI-Transformation als Grenzfall für Geschwindigkeiten, die klein gegen die Lichtgeschwindigkeit sind, enthalten sein. Das System S' soll sich mit der Geschwindigkeit v gegenüber einem System S in positiver x-Richtung bewegen.
Die GALILEI-Transformation für die x-Koordinate lautet dann in verallgemeinerter Form:

$x=k(x\text{'}+v\cdot t\text{'})\text{(1)}$

k ist dabei ein zu bestimmender Korrektorfaktor. Wegen der Gleichberechtigung der Bezugssysteme (Relativitätsprinzip) gilt aus der Sicht von S':

$x\text{'}=k(x-v\cdot t)\text{(2)}$

Für die anderen Koordinaten gilt y = y' und z = z'. Zum Zeitpunkt t = t' = 0 fallen die beiden Ursprünge der Koordinatensysteme zusammen. Wird zu diesem Zeitpunkt vom gemeinsamen Koordinatenursprung ein Lichtsignal ausgesandt, so gilt für den in beiden Systemen zurückgelegten Weg wegen der Konstanz der Lichtgeschwindigkeit:

$x=c\cdot t\text{und}x\text{'}=c\cdot t\text{'}\text{(3)}$

Die Transformationsgleichungen (1) und (2) müssen grundsätzlich auch auf den Vorgang der Lichtausbreitung anwendbar sein. Setzt man (1) und (2) in (3) ein, so ergibt sich:

$\begin{array}{l}c\cdot t=k(c\cdot t\text{'}+v\cdot t\text{'})=k(c+v)t\text{'}\\ \text{und}\\ c\cdot t\text{'}=k(c\cdot t-v\cdot t)=k(c-v)t\end{array}$

Die seitenweise Multiplikation dieser beiden Gleichungen ergibt:

$\begin{array}{l}{c}^2\cdot t\cdot t\text{'}=k^2(c+v)(c-v)t\cdot t\text{'}\\ \text{oder nach Division durch}t\cdot t\text{'}\text{und Ausmultiplizieren der Klammern:}\\ c^2=k^2(c^2-v^2)\\ \text{Die Umstellung nach}k\text{ergibt:}\\ k^2=\frac{c^2}{c^2-v^2}=\frac{c^2}{c^2(1-v^2/c^2)}=\frac{1}{1-v^2/c^2}\\ \text{Damit erhält man für}k:\\ k=\frac{1}{\sqrt{1-v^2/c^2}}\end{array}$

Das Einsetzen des Faktors k in die Gleichungen (1) bzw. (2) ergibt die Gleichungen für die LORENTZ-Transformation für x und x', die in der Übersicht oben genant sind. Das ebenfalls mögliche negative Vorzeichen bei k entspricht einer Spiegelung der Koordinaten.
Die Transformationsgleichung für die Zeit ergibt sich folgendermaßen: Gleichung (3) wird nach t' aufgelöst. Dann erhält man:

$t\text{'}=\frac{x\text{'}}{c}$

Setzt man für x' Gleichung (2) ein, so ergibt sich:

$\begin{array}{l}t\text{'}=\frac{k(x-v\cdot t)}{c}=k(\frac{x}{c}-\frac{v\cdot t}{c})=k(\frac{x}{c}-\frac{v\cdot t\cdot c}{c^2})\\ \text{Mit}\frac{x}{c}=t\text{und}t\cdot c=x\text{erhält man:}\\ t\text{'}=k(t-\frac{v}{c^2}x)\text{und mit}k=\frac{1}{\sqrt{1-v^2/c^2}}\\ t\text{'}=\frac{t-\frac{v}{c^2}x}{\sqrt{1-v^2/c^2}}\end{array}$

In analoger Weise kann man die Gleichung für t ableiten.

Herleitung der LORENTZ-Transformation aus einem MINKOWSKI-Diagramm

Eine Herleitung der LORENTZ-Transformation kann auch aus einem Minkowski-Diagramm (Raum-Zeit-Diagramm) erfolgen. Dazu stellen wir ein Ereignis A in einem Minkowski-Diagramm dar. Dieses Ereignis ist im Diagramm ein Punkt. Beschreiben lässt es sich durch die Koordinaten (x, t) im System S bzw. (x', t') im System S'. Das System S' bewegt sich gegenüber dem System S mit der Geschwindigkeit v in x-Richtung. Zum Zeitpunkt t = t' = 0 fallen die Ursprünge der Koordinatensysteme zusammen.
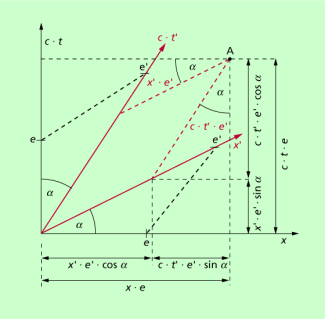
Damit man bei beiden Achsen mit Strecken arbeiten kann, wird auf der vertikalen Achse nicht t, sondern das Produkt $c\cdot t$aufgetragen. Analog wird das für die betreffende Achse im System S' gemacht. Eine Einheit auf der Achse nennen wir e im System S bzw. e' im System S'. Unter diesen Voraussetzungen erhält man das in Bild 3 dargestellte MINKOWSKI-Diagramm.
Dann erhält man für die Strecken die folgenden Ausdrücke (vgl. Bild 3):

$\begin{array}{l}x\cdot e=x\text{'}\cdot e\text{'}\cdot \cos \alpha +c\cdot t\text{'}\cdot e\text{'}\cdot \sin \alpha \text{(1)}\\ c\cdot t\cdot e=x\text{'}\cdot e\text{'}\cdot \sin \alpha +c\cdot t\text{'}\cdot e\text{'}\cdot \cos \alpha \text{(2)}\end{array}$

Diese Ausdrücke müssen nun umgeformt werden. Die Division durch e und Ausklammern auf der rechten Seite ergibt:

$\begin{array}{l}x=\frac{e\text{'}}{e}\cdot \cos \alpha (x\text{'}+c\cdot t\text{'}\cdot \tan \alpha )\text{(1a)}\\ c\cdot t=\frac{e\text{'}}{e}\cdot \cos \alpha (x\text{'}\cdot \tan \alpha +c\cdot t\text{'})\text{(2a)}\end{array}$

$\begin{array}{l}\text{Für die Einheiten auf den Achsen gilt die Beziehung}\\ \frac{e\text{'}}{e}=\frac{\sqrt{1+v^2/c^2}}{\sqrt{1-v^2/c^2}}\\ \text{und für den Winkel cos}\alpha \text{kann man schreiben:}\\ \text{cos}\alpha =\frac{1}{\sqrt{1+v^2/c^2}}\\ \text{Damit erhält man:}\\ \frac{\text{e'}}{\text{e}}\cdot \cos \alpha =\frac{\sqrt{1+v^2/c^2}}{\sqrt{1-v^2/c^2}}\cdot \frac{1}{\sqrt{1+v^2/c^2}}=\frac{1}{\sqrt{1-v^2/c^2}}\\ \text{Setzt man den rechts stehenden Ausdruck und darüber hinaus für}\\ \text{tan}\alpha =\frac{v}{c}\text{in die Gleichungen (1a) und (2a) ein}\text{, so erhält man:}\\ x=\frac{x\text{'}+v\cdot t\text{'}}{\sqrt{1-v^2/c^2}}=k(x\text{'}+v\cdot t\text{'})\text{(1b)}\\ t=\frac{t\text{'}+\frac{v}{c^2}x\text{'}}{\sqrt{1-v^2/c^2}}=k(t\text{'}+\frac{v}{c^2}x\text{'})\text{(2b)}\end{array}$

Die Gleichungen (1b) und (2b) sind die gesuchten Transformationsgleichungen für die Transformation vom System S' in das System S. Nach x' bzw. t' aufgelöst erhält man die entsprechenden Gleichungen für die Umrechnung vom System S in das System S'. Sie lauten:

$\begin{array}{l}x\text{'}=\frac{x-v\cdot t}{\sqrt{1-v^2/c^2}}=k(x-v\cdot t)\\ t\text{'}=\frac{t-\frac{v}{c^2}x}{\sqrt{1-v^2/c^2}}=k(t-\frac{v}{c^2}x)\end{array}$