Ort und Weg
Wichtige Größen zur Beschreibung der Bewegung von Körpern sind der Ort und der Weg, den ein Körper zurücklegt.
Unter dem Ort x, an dem sich ein Körper befindet, versteht man seine Lage in einem Bezugssystem zu einem bestimmten Zeitpunkt. Der Ort kann sich mit der Zeit ändern.
Der davon zu unterscheidende Weg s gibt an, wie groß die Länge der Bahn zwischen zwei Orten bei einer Bewegung ist.
Beide Größen, Ort und Weg, sind eng miteinander verbunden, aber nicht identisch, wie nachfolgend erläutert wird.
Die physikalische Größe Ort
Ob sich ein Körper bewegt oder ob er in Ruhe ist, hängt von dem Bezugssystem ab, das man den Betrachtungen zugrunde legt. Will man den Ort eines Körpers angeben, so benötigt man ebenfalls ein Bezugssystem.
Die Lage, die ein Körper in einem Bezugssystem zu einem bestimmten Zeitpunkt hat, wird als sein Ort bezeichnet.
Formelzeichen: x
Einheit: ein Meter (1 m)
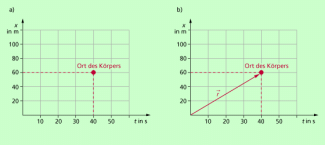
Die obige Festlegung ist deshalb zweckmäßig, weil man sich in der Kinematik zumeist auf die Bewegung in einer Raumrichtung beschränkt und dazu die x-Richtung auswählt. Damit ergibt sich der Ort als x-Koordinate in einem x-t-Diagramm. Zu seiner Beschreibung gibt es zwei Möglichkeiten (Bild 1):
a) In einem x-t-Diagramm ist der Ort x zu einem bestimmten Zeitpunkt t gleich der entsprechenden x-Koordinate (Bild 1a).
b) Die Lage eines Körpers lässt sich mithilfe eines Ortsvektors beschreiben, so wie das in Bild 1b dargestellt ist. Dann ist der Ort zu einem bestimmten Zeitpunkt durch die Einheitsvektoren in den Achsenrichtungen und die Koordinaten bestimmt.
Bei manchen Bewegungen, beispielsweise bei Würfen, ist es auch sinnvoll, die Bewegung nicht nur in einer Raumrichtung, sondern in einer Ebene zu betrachten. Dann wird der Ort durch die Koordinaten x und y zu einem bestimmten Zeitpunkt bestimmt.
-
Der Ort, an dem sich ein Körper in einem Bezugssystem befindet, kann in unterschiedlicher Weise angegeben werden.
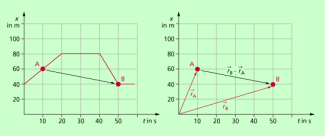
Die Ortsveränderung lässt sich ebenfalls entweder in einem Ort-Zeit-Diagramm mithilfe der Koordinaten oder mithilfe der Ortsvektoren beschreiben, so wie das in Bild 2 dargestellt ist. Diese Ortsveränderung muss nicht identisch mit dem Weg sein, der zwischen den betreffenden Punkten zurückgelegt wurde. Es gibt übrigens auch im täglichen Leben viele Beispiele, bei denen ein Körper in einem Zeitraum einen beträchtlichen Weg zurücklegt, sich aber schließlich zu irgendeinem Zeitpunkt wieder am Ausgangsort befindet. Man denke nur an die eigene Bewegung, z.B. von der Wohnung in die Schule und von dort zurück zur Wohnung.
Bei Fahrzeugen lässt sich heute der Ort mithilfe eines (GPS) bis auf wenige Meter genau bestimmen. Zu diesem Thema sind ausführliche Informationen in einem gesonderten Beitrag auf der CD enthalten.
-
Die Ortsveränderung lässt sich mithilfe von x-t-Diagrammen darstellen.
Die physikalische Größe Weg
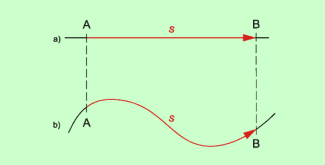
Körper bewegen sich längs einer bestimmten Bahn und legen dabei einen Weg zurück. Der Weg zwischen zwei Punkten A und B kann dabei je nach der Bahn unterschiedlich sein (Bild 2).
Der Weg gibt an, wie groß die Entfernung zwischen zwei Punkten längs der Bahn bei einer Bewegung ist.
Formelzeichen: s
Einheit: ein Meter (1 m)
Die Einheit Meter ist eine Basiseinheit des Internationalen Einheitensystems (SI). Ein Meter ist die Länge der Strecke, die Licht im Vakuum während der Dauer von 1/299.792.458 Sekunden durchläuft.
-
Der Weg zwischen zwei Punkten A und B kann unterschiedlich lang sein.
Messen des Weges oder der Länge
Wege oder Längen können mit verschiedenen Messgeräten gemessen werden, z. B. mit Linealen oder Messschiebern (Bild 4). Dabei ist zu beachten, dass jedes dieser Messgeräte eine Fertigungstoleranz hat und bei Messungen auch noch Messfehler hinzukommen. Beide addieren sich zum Größtfehler bei der Messung.
-
Die Länge kann mit unterschiedlichen Messgeräten (Lineal, Messschieber, Mikrometerschraube, Bandmaß) gemessen werden.

B. Mahler, Fotograf, Berlin
Bei Fahrzeugen wird der Weg mit Kilometerzählern oder beim Fahrrad auch mit Fahrradcomputern gemessen (Bild 5). Die Genauigkeit der Weg- oder Längenmessung hängt im Wesentlichen von dem verwendeten Messgerät ab. Während man mit einem handelsüblichen Lineal auf Millimeter genau messen und einen halben Millimeter schätzen kann, ist die Wegmessung bei Kilometerzählern in Fahrzeugen meist nur auf 100 m genau möglich.
Der Weg, der von einem Körper zurückgelegt wird, kann in einem Weg-Zeit-Diagramm dargestellt werden. Dabei ist zu beachten: Definiert man Ort und Weg so, wie oben geschehen, so ergeben sich daraus Konsequenzen für die entsprechenden Diagramme: Der Graph in einem Ort-Zeit-Diagramm kann beliebig verlaufen, auch in Form einer fallenden oder einer kreisförmigen Kurve. In einem Weg-Zeit-Diagramm muss der Graph einen positiven Anstieg oder den Anstieg null haben, denn auch wenn z.B. ein Fahrzeug zu seinem Ausgangspunkt zurückkehrt, vergrößert sich der von ihm zurückgelegte Weg.
Beachte: In manchen Materialien wird nicht zwischen Ort und Weg differenziert, sondern mit s manchmal der Ort und manchmal der Weg bezeichnet. Das ist möglich, führt aber mitunter zu Missverständnissen.
-
Die von einem Fahrzeug zurückgelegte Strecke kann man mit einem Kilometerzähler messen.

L. Meyer, Potsdam

