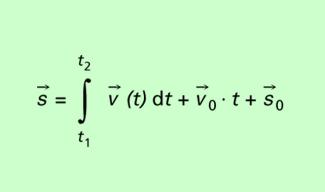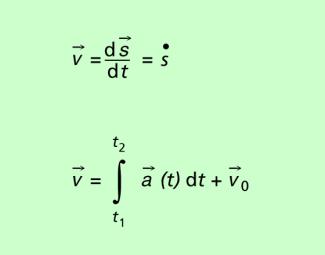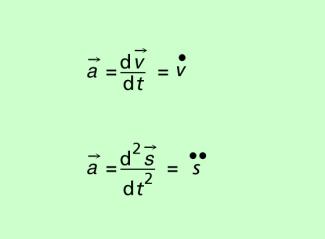Allgemeine Bewegungsgesetze

Die allgemeinen Bewegungsgesetze müssen so formuliert sein, dass zum einen der vektorielle Charakter von Weg, Geschwindigkeit und Beschleunigung berücksichtigt wird und darüber hinaus auch Anfangsweg und Anfangsgeschwindigkeit in die Betrachtungen einbezogen werden. Notwendig ist auch die Einbeziehung der Differenzial- und Integralrechnung.

Das Weg-Zeit-Gesetz

Beim Weg-Zeit-Gesetz ist zu beachten, dass die Geschwindigkeit eine Funktion der Zeit sein kann und dass eine Anfangsgeschwindigkeit und ein Anfangsweg zu berücksichtigen sind, die auch verschiedene Richtungen haben können. Das allgemeine Weg-Zeit-Gesetz lautet:

$\begin{array}{l}\overrightarrow{s}={\displaystyle \underset{t_1}{\overset{t_2}{\int }}\overrightarrow{v}(t)\text{d}t+{\overrightarrow{v}}_0}\cdot t+{\overrightarrow{s}}_0\\ \overrightarrow{v}\text{Geschwindigkeit}\\ {\overrightarrow{v}}_{\text{0}}\text{Anfangsgeschwindigkeit bei}t=0\\ {\overrightarrow{s}}_{\text{0}}\text{Anfangsweg bei}t=0\end{array}$

Haben Geschwindigkeit, Anfangsgeschwindigkeit und Anfangsweg die gleiche Richtung, dann kann man auch die Beträge schreiben. Liegen entgegengesetzte Richtungen vor, so wird das in der Betragsschreibweise durch ein Minuszeichen zum Ausdruck gebracht.

Beispiel: Geschwindigkeit und Anfangsweg haben die gleiche Richtung, die Anfangsgeschwindigkeit ist entgegengesetzt gerichtet. Dann lautet das Weg-Zeit-Gesetz:
$s={\displaystyle \underset{0}{\overset{t}{\int }}v(t)\text{d}t-v_0\cdot t+s_0}$
Spezialfälle lassen sich leicht ableiten, z.B. das Weg-Zeit-Gesetz für eine gleichmäßig beschleunigte Bewegung (a = konstant) ohne Anfangsweg und Anfangsgeschwindigkeit:

$\begin{array}{l}\text{Mit}{s}_0=0\text{und}{v}_0=0\text{sowie mit}v(t)=a\cdot t\\ \text{erhält man:}\\ s={\displaystyle \underset{0}{\overset{t}{\int }}a\cdot t\text{d}t}={\left[a\cdot \frac{t^2}{2}\right]}_0^t=\frac{a}{2}\cdot t^2\end{array}$

Das Geschwindigkeit-Zeit-Gesetz

Das allgemeine Geschwindigkeit-Zeit-Gesetz lässt sich in differenzieller Schreibweise oder in Integralschreibweise formulieren. Es lautet in den beiden Schreibweisen:
$\begin{array}{l}\overrightarrow{v}=\frac{\text{d}\overrightarrow{s}}{\text{d}t}=\stackrel{·}{s}\text{oder}\overrightarrow{v}={\displaystyle \underset{t_1}{\overset{t_2}{\int }}\overrightarrow{a}(t)\text{d}t+{\overrightarrow{v}}_0}\\ s\text{Weg}\\ t\text{Zeit}\\ a\text{Beschleunigung}\\ v_{\text{0}}\text{Anfangsgeschwindigkeit}\end{array}$

Der Punkt über dem s wird „s Punkt“ gesprochen und bedeutet in der Physik immer die 1. Ableitung der betreffenden Größe nach der Zeit. Welche Form zu bevorzugen ist, hängt von den gegebenen Bedingungen ab, wie die nachfolgenden Beispiele zeigen.

Beispiel 1:
Gegeben ist folgendes Weg-Zeit-Gesetz:
$s=\frac{a}{2}{t}^2-v_0\cdot t$
Wie lautet das betreffende Geschwindigkeit-Zeit-Gesetz?
Dieses Gesetz ergibt sich als 1. Ableitung des Weg-Zeit-Gesetzes nach der Zeit:
$\begin{array}{l}v=\frac{\text{d}s}{\text{d}t}\\ v=\frac{\text{d}(\frac{a}{2}\cdot t^2-v_0\cdot t)}{\text{d}t}\\ v=a\cdot t-v_0\end{array}$

Beispiel 2:
Eine Bewegung erfolgt mit einer konstanten Beschleunigung a. Zum Zeitpunkt

$\begin{array}{l}{t}_1=0\text{beträgt die Anfangsgeschwindigkeit}{v}_0.\\ \text{Die Richtung von}{v}_{\text{0}}\text{stimmt mit der von}a\text{überein}\text{.}\\ \text{Wie groß ist die Geschwindigkeit zum Zeitpunkt}{t}_2=t?\end{array}$
Kennt man Beschleunigung und Anfangsbedingungen, dann kann man das Geschwindigkeit-Zeit-Gesetz durch Integration ermitteln:

$\begin{array}{l}v={\displaystyle \underset{0}{\overset{t}{\int }}a\text{d}t}+v_0\\ v=a\cdot t+v_0\end{array}$

Das Beschleunigung-Zeit-Gesetz

Beim Beschleunigung-Zeit-Gesetz gibt es eine allgemeine differenzielle Schreibweise, die sich auf die Geschwindigkeit oder den Weg bezieht:
$\overrightarrow{a}=\frac{\text{d}\overrightarrow{v}}{\text{d}t}=\stackrel{·}{v}\text{oder}\overrightarrow{a}=\frac{{\text{d}}^2\overrightarrow{s}}{\text{d}{t}^2}=\stackrel{··}{s}$

Die Beschleunigung ist also die 1. Ableitung der Geschwindigkeit nach der Zeit oder die 2. Ableitung des Weges nach der Zeit. Kennt man für eine Bewegung das Weg-Zeit-Gesetz oder das Geschwindigkeit-Zeit-Gesetz, so kann man die Beschleunigung ermitteln, indem man die entsprechende Ableitung bildet.