Gleichförmige Kreisbewegung
Eine gleichförmige Kreisbewegung liegt vor, wenn sich ein Körper immer mit dem gleichen Betrag der Geschwindigkeit auf einer kreisförmigen Bahn bewegt.
Die gleichförmige Kreisbewegung ist eine beschleunigte Bewegung, da sich ständig die Richtung der Geschwindigkeit ändert.
Gleichförmige Kreisbewegung
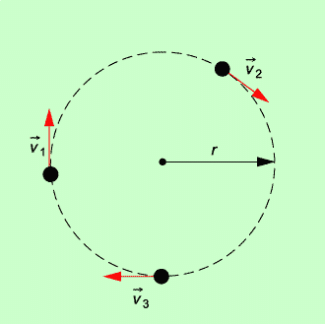
Eine gleichförmige Kreisbewegung liegt vor, wenn sich ein Körper immer mit dem gleichen Betrag der Geschwindigkeit auf einer kreisförmigen Bahn bewegt (Bild 1). Bei einer solchen gleichförmigen Kreisbewegung ändert sich aber ständig die Richtung der Geschwindigkeit.
-

L. Meyer, Potsdam
Eine gleichförmige Kreisbewegung ist deshalb stets eine beschleunigte Bewegung. Für eine gleichförmige Kreisbewegung (Bild 2) gelten folgende Gesetze:
| Dabei bedeuten: | v | Geschwindigkeit |
| s | Weg | |
| t | Zeit | |
| r | Radius der Kreisbahn | |
| T | Zeit für einen Umlauf (Umlaufzeit) | |
| n | Drehzahl |
Damit sich ein Körper gleichförmig auf einer Kreisbahn bewegt, muss auf ihn eine konstante Kraft in Richtung des Drehzentrums wirken. Diese Kraft wird als Radialkraft und manchmal auch als Zentralkraft oder als Zentripetalkraft bezeichnet.
Genauere Informationen dazu sind unter dem Stichwort „Kräfte bei der Kreisbewegung“ zu finden. Die durch die Radialkraft auftretende ständige Beschleunigung in Richtung Zentrum der Kreisbewegung wird als Radialbeschleunigung bezeichnet. Eine Ableitung dieser Größe findet man in dem Beitrag „Beschleunigung“. Für die Radialbeschleunigung gilt:
Mit dem newtonschen Grundgesetz ergibt sich mit dieser Beschleunigung für die Radialkraft: