Gleichförmige Drehbewegung
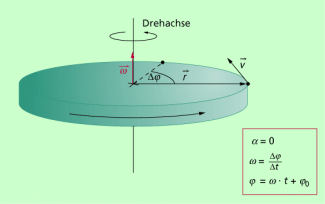
Eine gleichförmige Drehbewegung liegt vor, wenn ein starrer Körper mit konstanter Winkelgeschwindigkeit rotiert. Beispiele dafür sind ein Riesenrad oder eine mit bestimmter Drehzahl rotierende Motorwelle. Die dafür geltenden Gesetze sind analog zu den Gesetzen für die gleichförmige Bewegung bei der Translation:
Weitere Beispiele für solche gleichförmigen Drehbewegungen sind ein mit bestimmter Drehzahl rotierendes Schwungrad, der Rotor eines Generators, die Zeiger einer Uhr oder die Erde, die gleichförmig um ihre Achse rotiert. Es gilt also:
Eine gleichförmige Drehbewegung ist die Bewegung eines starren Körpers um eine Drehachse mit konstanter Winkelgeschwindigkeit, mit konstanter Drehzahl oder mit konstanter Umlaufzeit.
Dabei ist zu beachten, dass man bei einem starren Körper von einer Drehbewegung spricht. Ein einzelner Punkt eines solchen starren Körpers führt dagegen eine Kreisbewegung aus.
-

MEV Verlag, Augsburg
Gesetze für die gleichförmige Drehbewegung
Für eine gleichförmige Drehbewegung gelten die analogen Gesetze wie für die gleichförmige Bewegung bei der Translation:
Die Winkelbeschleunigung ist null:
Die Winkelgeschwindigkeit ist gleich der Änderung des Drehwinkels in der Zeiteinheit:
Die Winkelgeschwindigkeit kann man auch mithilfe der Umlaufzeit T (Zeit für einen vollen Umlauf) oder durch die Drehzahl n (Anzahl der Umdrehungen in der Sekunde) ausdrücken. Beide Größen sind bei einer gleichförmigen Kreisbewegung konstant:
Der Drehwinkel hängt von der Winkelgeschwindigkeit ab. Für ihn gilt:
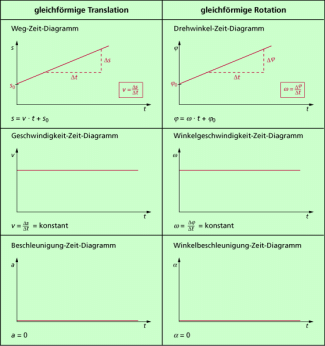
Diese Zusammenhänge lassen sich auch grafisch darstellen. Die entsprechenden grafischen Darstellungen sind in Bild 3 angegeben. Zum Vergleich sind die entsprechenden Diagramme für die gleichförmige Bewegung bei einer Translation mit dargestellt.
Winkelgeschwindigkeit und Bahngeschwindigkeit
Mit welcher Geschwindigkeit sich einzelne Punkte des rotierenden starren Körpers längs ihrer (kreisförmigen) Bahn bewegen, hängt von der Winkelgeschwindigkeit und von seiner Entfernung r von der Drehachse ab. Für die Bahngeschwindigkeit v eines Massepunktes gilt: