Quantenmechanisches Atommodell

Der Weg zum quantenmechanischen Atommodell

Auch erschienen die von BOHR aufgestellten Postulate recht willkürlich und nicht als logische Ableitungen aus theoretischen Positionen.

Insbesondere jüngere Quantenphysiker wie ERWIN SCHRÖDINGER (1887-1961), WERNER HEISENBERG (1901-1976) und MAX BORN (1882-1970) leisteten in den zwanziger Jahren wichtige Beiträge zur Weiterentwicklung der Quantenphysik und schufen so auch die theoretischen Grundlagen für eine moderne Atomtheorie. Insbesondere war das Problem zu lösen, einerseits die diskreten Energieniveaus der Atome zu berechnen und andererseits auf die Vorstellung von Elektronenbahnen zu verzichten.

Das Wesen des quantenmechanischen Atommodells

Eine entscheidende Grundlage des weiterentwickelten Atommodells waren Erkenntnisse der Quantentheorie, insbesondere die von dem österreichischen Physiker ERWIN SCHRÖDINGER (1887-1961) 1926 aufgestellte SCHRÖDINGER-Gleichung, für die er 1933 den Nobelpreis für Physik erhielt.
Das Problem ist hierbei, dass es sich um ein mathematisches Modell handelt und damit alle bildhaften Darstellungen problematisch sind und nicht selten zu falschen Vorstellungen führen. Die Grundidee von SCHRÖDINGER war, Elektronen nicht als diskrete Teilchen, sondern als Wellen aufzufassen. Nach der von DE BROGLIE aufgestellten Beziehung erhält man für die Wellenlänge:
$\lambda =\frac{h}{m\cdot v}$
Die Wellenlänge muss im einfachsten Falle so groß sein, dass genau eine ganze Anzahl von Wellenlängen auf den Bahnumfang entfällt, also eine stehende Welle vorhanden ist. Für diesen Fall würde dann gelten:
$\begin{array}{l}2\pi \cdot r=n\cdot \lambda \text{und mit}\lambda =\frac{h}{m\cdot v}:\\ 2\pi \cdot r=n\cdot \frac{h}{m\cdot v}\text{oder}\\ 2\pi \cdot r\cdot m\cdot v=n\cdot h\text{mit}n=\mathrm{1,}\mathrm{2,}\mathrm{...}\end{array}$

Ganz zwanglos ergibt sich damit die bohrsche Quantenbedingung.

Der um den Atomkern laufende Wellenzug und die Ausbildung einer stehenden Welle ist ein stark vereinfachtes Bild. Erwin Schrödinger führte diesen Gedankengang weiter und dachte sich statt des um den Kern laufenden Elektrons ein räumlich ausgedehntes Gebilde, das ebenfalls in Form einer stehenden Welle schwingen kann. Die von ihm dafür entwickelte Grundgleichung - die SCHRÖDINGER-Gleichung - lautet:
$\begin{array}{l}\Delta \psi =\frac{1}{u^2}\cdot \frac{{\partial }^2\psi }{\partial t^2}\\ \psi \text{Amplitude des schwingenden Gebildes}\\ u\text{Geschwindigkeit der sich überlagernden Wellen}\end{array}$
Die physikalische Bedeutung der Psi-Funktion wurde insbesondere von MAX BORN herausgearbeitet: Das Absolutquadrat dieser Wellenfunktion ist als Wahrscheinlichkeitsdichte für das Auffinden eines Teilchens zur Zeit t an einem bestimmten Ort r zu deuten.

Damit kann man Wahrscheinlichkeiten berechnen, ein Elektron in einem gewissen Abstand vom Atomkern anzutreffen. Diese so berechneten Wahrscheinlichkeiten müssen einer Normierungsbedingung genügen. Diese besagt: Ein Elektron befindet sich mit der Wahrscheinlichkeit w = 1 irgendwo in der Atomhülle. Löst man die SCHRÖDINGER-Gleichung für das Wasserstoffatom auf, so lassen sich nur solche Lösungen normieren, die der Energie von Elektronen mit folgenden Werten entsprechen:
$\begin{array}{l}{E}_{\text{n}}=\frac{h\cdot R_{\text{y}}}{n^2}\\ E_{\text{n}}\text{Energie des}n\text{-ten Niveaus}\\ h\text{plancksches Wirkungsquantum}\\ R_{\text{y}}\text{RYDBERG-Frequenz}\\ n\text{Hauptquantenzahl (}n=\mathrm{1,}\mathrm{2,}\mathrm{...})\end{array}$

Das sind genau die diskreten Energieniveaus, die beim Wasserstoff ermittelt wurden.

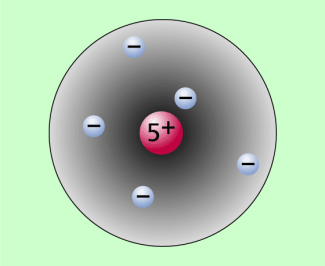
Die räumlichen Wahrscheinlichkeitsverteilungen der Elektronen in der Atomhülle werden als Orbitale bezeichnet (Bild 4). Davon ausgehend bezeichnet man das quantenmechanische Atommodell auch als Orbitalmodell. Wie genaue Berechnungen zeigen, können bis auf den Grundzustand zu einer bestimmten Hauptquantenzahl n mehrere, voneinander verschiedene räumliche Wahrscheinlichkeitsverteilungen existieren.

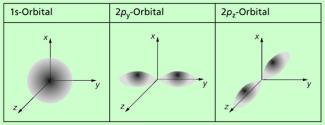
Diese verschiedenen Orbitale klassifiziert man durch sogenannten Nebenquantenzahlen l und m. Darüber hinaus kann ein Elektron unabhängig von seiner Wahrscheinlichkeitsverteilung im Raum selbst zwei Energiezustände annehmen, die durch die Spinquantenzahl s charakterisiert werden. Experimentell nachgewiesen wurde der Elektronenspin 1921 mit dem STERN-GERLACH-Versuch. Die Physiker OTTO STERN (1888-1969) und WALTHER GERLACH (1889-1979) schickten Atome als Strahl durch ein Magnetfeld. Dabei erfolgte eine Aufteilung in zwei oder mehrere Strahlen, je nach dem vorhandenen magnetischen Moment.
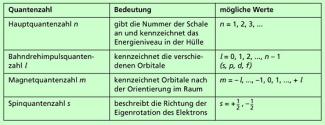
Zusammenfassend dargestellt sind die vier Quantenzahlen in der in Bild 5 dargestellten Übersicht.