Räumliche Verteilung von Teilchen
Gegenstand der kinetischen Gastheorie ist die Betrachtung thermodynamischer Prozesse auf der Grundlage von Teilchengrößen, wie der Teilchenanzahl, ihrer Geschwindigkeit und ihrer Energie. Von Interesse ist auch die räumliche Verteilung von Teilchen eines Gases in verschiedenen Raumbereichen eines abgeschlossenen Systems. Bei einer hinreichend großen Anzahl von Teilchen ist für ein abgeschlossenes System die Gleichverteilung die wahrscheinlichste räumliche Anordnung. Es können aber auch statistische Schwankungen auftreten, die sich z.B. in Dichteunterschieden bemerkbar machen.
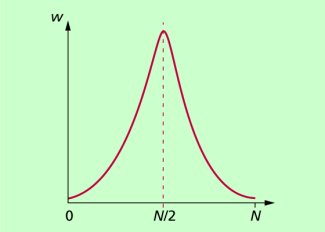
Wir betrachten zwei Raumbereiche, die durch eine Wand voneinander betrennt sind. In dem einen Raumbereich befinden sich zunächst alle Teilchen, in dem anderen gar keins (Bild 1 a).
Beseitigt man die Trennwand, dann verteilen sich die Teilchen im gesamten zur Verfügung stehenden Volumen (Bild 1b).
Geht man von einer großen Teilchenanzahl aus, wie das bei makroskopischen Systemen der Fall ist, dann gilt:
Die Gleichverteilung der Teilchen ist die wahrscheinlichste räumliche Anordnung in einem gegebenen Raumbereich.
Dieser Sachverhalt lässt sich auch über die Teilchenanzahldichte ausdrücken, also durch die Teilchenanzahl N im Volumen V:
Eine konstante Teilchenanzahldichte N/V ist der wahrscheinlichste Zustand in einem gegebenen Raumbereich.
Unter der Wahrscheinlichkeit w einer Verteilung versteht man die relative Häufigkeit des Auftretens einer Verteilung. Die Wahrscheinlichkeit, dass sich ein beliebiges Teilchen im Gesamtvolumen befindet, ist w = 1. Das gilt auch für 2 oder für n Teilchen. Dagegen ist die Wahrscheinlichkeit, dass sich ein bestimmtes Teilchen im halben Volumen befindet, nur
Das gilt auch für ein zweites Teilchen. Die Wahrscheinlichkeit, beide Teilchen gleichzeitig in diesem
Auch an der Wahrscheinlichkeit zeigt sich: Mit zunehmender Teilchenanzahl wird die Wahrscheinlichkeit, Teilchen im gleichen Raumbereich zu finden, immer geringer. Die Verteilung unterliegt einem statistischen Gesetz.
-
Teilchen eines Gases verteilen sich gleichmäßig in dem zur Verfügung stehenden Raum.
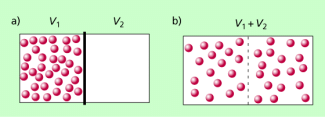
Stellt man die Wahrscheinlichkeit der Verteilung von N Teilchen in zwei gleich großen Raumbereichen grafisch dar, so ergibt sich die in Bild 2 dargestellte Kurve, die so zu interpretieren ist:
- Die Wahrscheinlichkeit, dass sich in jedem der beiden Raumbereiche N/2 Teilchen befinden ist besonders groß.
- Andere Zustände als die Gleichverteilung sind möglich. Ihre Wahrscheinlichkeit ist aber umso kleiner, je weiter sie von der Gleichverteilung entfernt sind.
- Die Wahrscheinlichkeit dafür, dass sich in einem der beiden Raumbereiche alle oder kein Teilchen befindet, geht gegen null. Betrachtet man beispielsweise die Anzahl der Moleküle in einem Kubikzentimeter Luft unter Normbedingungen, dann sind das
Abweichungen von den statistisch wahrscheinlichsten Zuständen werden als statistische Schwankungen oder Schwankungserscheinungen bezeichnet. Eine solche statistische Schwankung ist die brownsche Bewegung. Statistische Schwankungen spielen auch bei hochempfindlichen Messgeräten eine Rolle. So begrenzen z.B. statistische Stromschwankungen die Empfindlichkeit elektronischer Bauteile.
-
Wahrscheinliche Verteilung von N Teilchen in zwei Raumbereichen