Das gilt auch für rotierende starre Körper, z.B. Schwungräder, die Rotoren von Generatoren und Motoren, rotierende Räder oder einen Kreisel.

Die Energie, die ein rotierender starrer Körper besitzt, wird als Rotationsenergie bezeichnet.

Herleitung der Gleichung

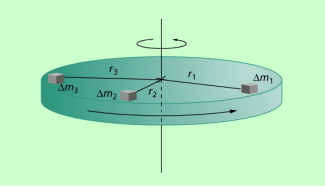
Die Gleichung für die Rotationsenergie ergibt sich aus folgender Überlegung: Jedes Masseelement eines rotierenden starren Körpers besitzt eine bestimmte kinetische Energie, die von der Masse selbst und von der Geschwindigkeit abhängig ist (Bild 2). Die Geschwindigkeit wiederum hängt bei bestimmter Winkelgeschwindigkeit vom Abstand von der Drehachse ab:

$\begin{array}{l}{E}_i=\frac{1}{2}\Delta m_i\cdot v_i^2\text{und mit}{v}_i=\omega \cdot r_i\\ E_i=\frac{1}{2}\Delta m_i\cdot {\omega }^2\cdot r_1^2\end{array}$

Die Gesamtenergie, die dann als Rotationsenergie des Körpers bezeichnet wird, ergibt sich als Summe der kinetischen Energien aller Masseelemente:

$\begin{array}{l}{E}_{rot}={\displaystyle \sum _{i=1}^n{E}_i}=\frac{1}{2}{\omega }^2\cdot {\displaystyle \sum _{i=1}^n\Delta m_i\cdot r_1^2}\\ \text{Der Term}{\displaystyle \sum _{i=1}^n\Delta m_i\cdot r_1^2}\text{ist das Trägheitsmoment}J.\\ \text{Demzufolge erhält man:}\\ E_{rot}=\frac{1}{2}J\cdot {\omega }^2\end{array}$

Ein Beispiel für die Anwendung

Als Beispiel betrachten wir eine Kugel, die eine geneigte Ebene der Höhe h hinabrollt. Für eine solche Kugel kann man z.B. untersuchen, welche Energie sie besitzt und welche Geschwindigkeit sie erreicht, wenn sie die Höhe h hinabrollt.

Wir nehmen an, dass die Kugel mit der Masse m in der Höhe h zunächst ruht. Sie hat dann potenzielle Energie:
$E_{pot}=m\cdot g\cdot h$
Beim Hinabrollen wandelt sich diese potenzielle Energie in kinetische Energie um, wobei sich diese kinetische Energie aus zwei Anteilen zusammensetzt: Zum einen führt der Schwerpunkt der Kugel eine Translation aus. Die Kugel hat damit kinetische Energie der Translation. Zugleich rotiert die Kugel, hat also auch Rotationsenergie:
$E_{Bewegung}=E_{kin}+E_{rot}=\frac{1}{2}m\cdot v^2+\frac{1}{2}J\cdot {\omega }^2$
Vernachlässigt man die Reibung, dann gilt der Energieerhaltungssatz der Mechanik. Die gesamte potenzielle Energie wird in Bewegungsenergie umgewandelt:
$\begin{array}{l}m\cdot g\cdot h=\frac{1}{2}m\cdot v^2+\frac{1}{2}J\cdot {\omega }^2\\ \text{Setzt man in diese Gleichung das Trägheitsmoment einer}\\ \text{Kugel}\left(J=\frac{2}{5}m\cdot r^2\right)\text{ein}\text{, so erhält man:}\\ m\cdot g\cdot h=\frac{1}{2}m\cdot v^2+\frac{1}{2}\cdot \frac{2}{5}m\cdot r^2\cdot {\omega }^2\\ \text{Mit}\omega =\frac{v}{r}\text{erhält man:}\\ m\cdot g\cdot h=\frac{1}{2}m\cdot v^2+\frac{2}{10}m\cdot v^2\\ \text{Die Division durch}m\text{und die Umstellung nach}v\text{ergibt:}\\ v=\sqrt{\frac{10}{7}g\cdot h}\end{array}$
Das wäre die Geschwindigkeit einer Kugel beim Hinabrollen, wenn die Ausgangshöhe h wäre. Sie ist unabhängig von der Masse der Kugel. Die Geschwindigkeit einer Kugel ist kleiner als die eines reibungsfrei herabgleitenden Körpers $\left(v=\sqrt{2g\cdot h}\right)$. Das ist deshalb der Fall, weil bei einem solchen herabgleitenden Körper die gesamte potenzielle Energie in kinetische Energie der Translation umgewandelt wird. Bei rotierenden Körpern dagegen wird immer in Teil der potenziellen Energie in Rotationsenergie umgewandelt. Damit ist der Anteil der kinetischen Energie der Translation und damit auch auch die Geschwindigkeit kleiner.