Spezielle Zustandsänderungen
Aus der allgemeinen Zustandsgleichung für das ideale Gas kann man Gleichungen für den Fall ableiten, dass eine der drei Größen konstant ist. Mit p = konstant ergeben sich Gleichungen für die isobare Zustandsänderung, mit V = konstant für die isochore Zustandsänderung und mit T = konstant für die isotherme Zustandsänderung. Die Gleichungen für diese speziellen Zustandsänderungen wurde früher gefunden als der allgemeine Fall. Nach den Wissenschaftlern, die sie entdeckten, nennt man diese Gesetze auch das Gesetz von GAY-LUSSAC, das Gesetz von AMONTONS und das Gesetz von BOYLE und MARIOTTE.
Durch die allgemeine Zustandsgleichung für das ideale Gas in der Form
wird der Zusammenhang zwischen Druck, Volumen und Temperatur angegeben. Bei einer Reihe thermodynamischer Prozesse ist eine der drei Größen konstant. Man erhält dann drei spezielle Zustandsänderungen:
| Bezeichnung der Zustandsänderung | konstante Größe | veränderliche Größen |
| isobare Zustandsänderung | Druck p = konstant | Volumen V Temperatur T |
| isochore Zustandsänderung | Volumen V = konstant | Druck p Temperatur T |
| isotherme Zustandsänderung | Temperatur T = konstant | Druck p Volumen V |
Darüber hinaus gibt es noch die adiabatische Zustandsänderung, bei der sich alle drei Größen ändern.
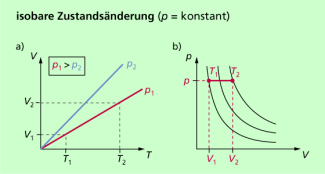
Die isobare Zustandsänderung
Isobare Zustandsänderungen sind dadurch gekennzeichnet, dass der Druck konstant ist. Aus der allgemeinen Zustandsgleichung für das ideale Gas erhält man mit p = konstant:
Nach seinem Entdecker JOSEPH LOUIS GAY-LUSSAC (1778-1850) wird dieses spezielle Gasgesetz auch als Gesetz von GAY-LUSSAC bezeichnet.
Im V-T-Diagramm (Bild 2a) ergeben sich Geraden, deren Anstieg vom Druck abhängig ist. Im p-V-Diagramm ergibt sich eine Gerade parallel zur V-Achse (Bild 2).
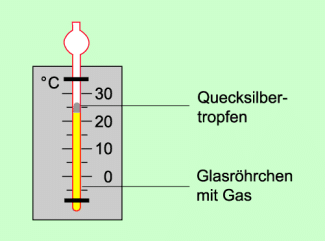
Die Volumenänderung bei Temperaturänderung wird z.B. bei einem Gasthermometer genutzt (Bild 3). In einem Glasröhrchen befindet sich ein Gas, im einfachsten Falle Luft. Das Gas ist durch einen Quecksilbertropfen abgeschlossen. Der Quecksilbertropfen wirkt mit seiner Gewichtskraft auf das eingeschlossene Gas. Dadurch besteht im Gas ein bestimmter, konstanter Druck.
Vergrößert sich die Temperatur, so vergrößert sich proportional dazu das Volumen des eingeschlossenen Gases. Der Quecksilbertropfen steigt demzufolge nach oben. Bei Verringerung der Temperatur verkleinert sich das Volumen des eingeschlossenen Gases. Der Quecksilbertropfen sinkt nach unten. Die Höhe des Quecksilbertropfens ist somit ein Maß für die jeweilige Temperatur. Bringt man eine Skala und eicht das Thermometer, so kann man die jeweilige Temperatur in Höhe des Quecksilbertropfens ablesen.
Bei einem Wohnraum ist der Druck gleich dem Luftdruck. Bei einer bestimmten Temperatur befindet sich in einem solchen Raum eine bestimmte Menge Luft. Wird durch Heizen die Temperatur erhöht, so nimmt die Luftmenge ein größeres Volumen ein. Da sich die Raumgröße nicht ändert, strömt ein Teil der Luft aus. Umgekehrt verringert sich bei Verringerung der Temperatur das Volumen einer bestimmten Gasmenge. In einen Raum würde dann von außen Luft einströmen.
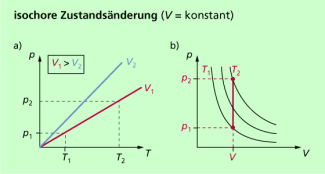
Die isochore Zustandsänderung
Isochore Zustandsänderungen sind dadurch gekennzeichnet, dass das Volumen konstant ist. Aus der allgemeinen Zustandsgleichung für das ideale Gas erhält man mit V = konstant:
Nach seinem Entdecker GUILLAUME AMONTONS (1663-1705) wird dieses spezielle Gasgesetz auch als Gesetz von AMONTONS bezeichnet.
Im p-T-Diagramm (Bild 4a) ergeben sich Geraden, deren Anstieg vom Volumen abhängig ist. Im p-V-Diagramm ergibt sich eine Gerade parallel zur p-Achse (Bild 4b).
Beispiele für das Wirken des Gesetzes von AMONTONS sind Gasflaschen, Spraydosen oder PKW-Reifen, in denen sich eine abgeschlossene Menge eines Gases befindet, das sich näherungsweise wie das ideale Gas verhält. Erhöht sich z. B. durch Sonneneinstrahlung oder durch andere Einwirkungen die Temperatur, so erhöht sich auch der Druck im Gas. Bei Gasflaschen und Spraydosen darf die Temperatur bestimmte Werte nicht übersteigen, weil sonst wegen der Erhöhung des Druckes mit der Temperatur Explosionsgefahr besteht. So sollte bei Spraydosen auf keinen Fall eine Temperatur von 50 °C überschritten werden. Wegen der Explosionsgefahr ist das lebensgefährlich.
Autoreifen dehnen sich aufgrund ihres Aufbaus kaum aus. Damit erhöht sich auch in ihnen mit steigender Temperatur der Druck. Eine Temperaturerhöhung und damit eine Druckerhöhung tritt nicht nur auf, wenn ein Fahrzeug in der prallen Sonne steht, sondern auch beim schnellen Fahren. Deshalb ist es nicht zweckmäßig, nach längeren Fahrten den Luftdruck zu kontrollieren. Die für Reifen empfohlenen Druckwerte beziehen sich immer auf den Reifendruck bei Umgebungstemperatur.
-

L. Meyer, Potsdam
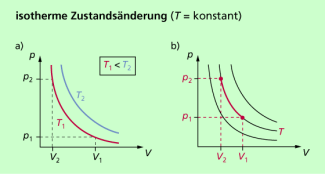
Die isotherme Zustandsänderung
Isotherme Zustandsänderungen sind dadurch gekennzeichnet, dass die Temperatur konstant ist. Aus der allgemeinen Zustandsgleichung für das ideale Gas erhält man mit T = konstant:
Nach seinen Entdeckern ROBERT BOYLE (1627-1691) und EDME MARIOTTE (um 1620-1684) wird dieses spezielle Gasgesetz auch als Gesetz von BOYLE und MARIOTTE bezeichnet.
Im p-V-Diagramm (Bild 6a) ergeben sich Kurven, deren Verlauf von der Temperatur abhängig ist. Für eine bestimmte Temperatur ergibt sich eine Kurve (Bild 6b).
Beispiele für das Wirken des Gesetzes von BOYLE und MARIOTTE treten überall dort auf, wo sich das Volumen abgeschlossener Gasmengen ändert und dabei die Temperatur näherungsweise konstant ist.
Ein Beispiel dafür sind Pumpen (Luftpumpen, Pumpen für Sauerstoff in der Medizin). Bei näherungsweise konstanter Temperatur wird das Volumen des Gases verringert. Dadurch erhöht sich der Druck in ihm. Bei einem bestimmten höheren Druck strömt das Gas in den gewünschten Raum, z. B. bei einer Luftpumpe in den Schlauch oder bei einer medizinischen Pumpe in die Lunge.
Auch bei Wasserbällen oder Luftmatratzen zeigt sich der Zusammenhang zwischen Druck und Volumen: Je mehr Luft man hineinbläst, desto größer wird der Druck. Mit Vergrößerung des Druckes vergrößert sich auch das Volumen.
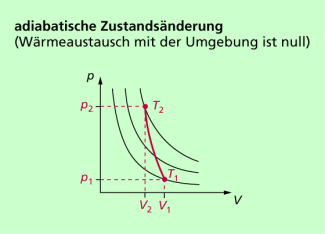
Die adiabatische Zustandsänderung
Adiabatische Zustandsänderungen sind dadurch gekennzeichnet, das sich zum einen die drei Größen Druck, Volumen und Temperatur ändern, dabei aber das Gas keine Wärme mit der Umgebung austauscht. Ein Beispiel für eine adiabatische Zustandsänderung ist in Bild 7 dargestellt.
Alle genannten speziellen Zustandsänderungen spielen z. B. bei den verschiedenen Kreisprozessen und bei Wärmekraftmaschinen eine Rolle. Genauere Informationen zu den damit verbundenen energetischen Vorgängen bei den einzelnen Zustandsänderungen sind in gesonderten Beiträgen unter „Isotherme Zustandsänderungen“, „Isobare Zustandsänderungen“, „Isochore Zustandsänderungen“ und „Adiabatische Zustandsänderungen“ zu finden.
Suche nach passenden Schlagwörtern
- isobare Zustandsänderungen
- Berechnung
- isotherme Zustandsänderungen
- Gasflaschen
- Gesetz von Amontons
- isochore Zustandsänderungen
- Gasthermometer
- Pumpen
- Simulation
- Rechenbeispiel
- Gesetz von Gay-Lussac
- Gesetz von Boyle und Mariotte
- spezielle Zustandsänderungen
- allgemeine Zustandsgleichung für das ideale Gas
- Autoreifen
- Spraydosen
- adiabatische Zustandsänderungen