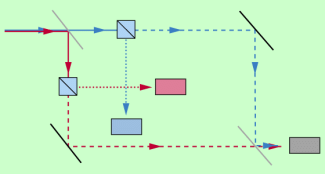
Welcher-Weg-Messung im Photonen-Interferometer
Bei Interferenzexperimenten ist es unbestimmt, welchen der klassisch denkbaren Wege die Quantenobjekte gehen. So gehen sie beim Doppelspaltexperiment nicht durch genau einen der Spalte, beim Interferometer-Experiment gehen sie nicht auf einem der zwei klassisch denkbaren Wege. Dies ist allerdings nur der Fall, solange man nicht misst, welchen „Weg“ das Quantenobjekt nimmt. Eine solche Messung kann man beim Interferometer mit der Methode der Photonenverdopplung machen.
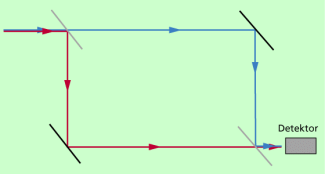
Das Interferometer und die zwei klassisch denkbaren Wege
Das Photon kann auf zwei Arten zum Detektor gelangen: Entweder wird es am ersten Strahlteiler reflektiert, am linken unteren Spiegel reflektiert und vom zweiten Strahlteiler (rechts unten) durchgelassen (blaue Linie) oder es wird vom ersten Strahlteiler durchgelassen, am rechten oberen Spiegel reflektiert und am zweiten Strahlteiler (rechts unten) reflektiert (rote Linie).
-
Das Interferometer und die zwei klassisch denkbaren Wege
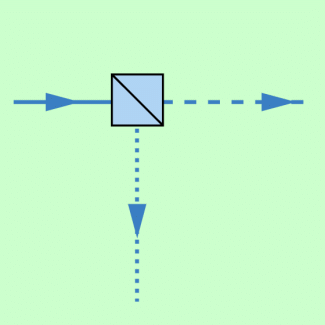
Photonenverdopplung im nichtlinearen Kristall
Es gibt sogenannte nichtlineare Kristalle, mit denen es gelingt, ein ankommendes Photon (durchgezogene Linie) in zwei Photonen kleinerer Frequenz (gestrichelte bzw. gepunktete Linie) aufzuspalten.
Welcher Weg-Messung durch Photonenverdopplung
In jeden der zwei Wege des Interferometers wird ein nichtlinearer Kristall gebracht. Wenn der blaue Detektor ein Signal gibt, dann weiß man, dass die blaue Möglichkeit realisiert wurde, ebenso beim roten. Mit dieser Anordnung kann also gemessen werden, ob die Variante oben herum (blau) oder unten herum (rot) gewählt wurde. Mit dieser Messung ist auch nicht mehr unbestimmt, welchen Weg das Photon wählt. Dies äußert sich darin, dass nun kein Interferenzmuster beobachtet werden kann (siehe Komplementaritätsprinzip: Welcher-Weg-Information und Interferenzmuster schließen sich aus).
-
Photonenverdopplung am nichtlinearen Kristall
-
Prinzipieller Versuchsaufbau von ZEILINGER et al.