Zentraler gerader elastischer Stoß

Ein zentraler elastischer Stoß zwischen zwei Körpern ist dadurch gekennzeichnet, dass

nur elastischen Wechselwirkungen auftreten,
sich die Körper nach dem Stoß mit unterschiedlichen Geschwindigkeiten weiterbewegen und
die mechanische Energie erhalten bleibt.

Für einen solchen Stoß gilt der Impulserhaltungssatz und der Energieerhaltungssatz der Mechanik.

Kim hat in Deutsch, Mathe, Englisch und 6 weiteren Schulfächern immer eine von Lehrkräften geprüfte Erklärung, Video oder Übung parat.
24/7 auf Learnattack.de und WhatsApp mit Bildupload und Sprachnachrichten verfügbar. Ideal, um bei den Hausaufgaben und beim Lernen von Fremdsprachen zu unterstützen.
Viel günstiger als andere Nachhilfe und schützt deine Daten.

Jetzt 30 Tage risikofrei testen

Kennzeichnung eines zentralen unelastischen Stoßes

Ein zentraler gerader unelastischer Stoß zwischen zwei Körpern ist dadurch gekennzeichnet, dass

die Verbindungsgerade der Schwerpunkte beider Körper senkrecht auf der Berührungsfläche steht, die sich beim Stoß ausbildet (zentraler Stoß),
beim Stoß nur elastischen Wechselwirkungen auftreten,
sich die Körper nach dem Stoß mit unterschiedlichen Geschwindigkeiten weiterbewegen und
die kinetische Energie vor dem Stoß genauso groß ist die kinetische Energie nach dem Stoß.

Beispiele für Stöße, die näherungsweise als solche zentralen elastischen Stöße angesehen werden können, sind der Schlag eines Tennisschlägers gegen einen Tennisball, der Aufprall eines hochelastischen Balles auf Steinfußboden, der Stoß von zwei Billardkugeln. Elastische Stöße treten auch bei Elementarteilchen auf.
Dabei ist aber stets zu beachten: Ein (ideal) elastischer Stoß ist eine Idealisierung, die in der Praxis nur näherungsweise auftritt. Damit muss für den jeweiligen Fall geprüft werden, ob die nachfolgend genannten Gesetze angewendet werden können.

Gesetze für den zentralen elastischen Stoß

Wir betrachten als Beispiel einen zentralen elastischen Stoß zwischen zwei Wagen. Durch die am Wagen befestigte Feder erfolgt beim Stoß eine elastische Wechselwirkung. Die gesamte Anordnung betrachten wir als ein abgeschlossenes System, vernachlässigen damit auch den Einfluss von Reibungseffekten. Experimentell kann man das realisieren, wenn man eine Luftkissenbahn nutzt, so wie das in zu sehen ist.

Für eine solche Anordnung gilt der Impulserhaltungssatz:

$m_{1} \cdot {\vec{v}}_{1} + m_{2} \cdot {\vec{v}}_{2} = m_{1} \cdot {\vec{u}}_{1} + m_{2} \cdot {\vec{u}}_{2}$

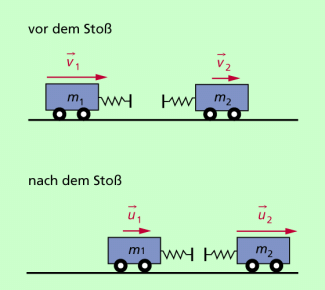
Für den Spezialfall des zentralen Stoßes bewegen sich die Körper längs einer Geraden und man kann die Impulsgleichung ohne Vektorpfeile schreiben. Dabei vereinbart man noch, dass Geschwindigkeiten nach rechts ein positives Vorzeichen bekommen, Geschwindigkeiten nach links ein negatives:

$m_{1} \cdot v_{1} + m_{2} \cdot v_{2} = m_{1} \cdot u_{1} + m_{2} \cdot u_{2}$ (1)

Ändern die Stoßpartner während ihrer Bewegung ihre Höhenlage nicht, wird zwischen ihnen also nur kinetische Energie ausgetauscht, dann lautet der Energieerhaltungssatz für den Stoßvorgang:

$\frac{1}{2} m_{1} \cdot v_{1}^{2} + \frac{1}{2} m_{2} \cdot v_{2}^{2} = \frac{1}{2} m_{1} \cdot u_{1}^{2} + \frac{1}{2} m_{2} \cdot u_{2}^{2}$ (2)

Mit den Gleichungen (1) und (2) für den Impuls und die Energie stehen zwei Gleichungen mit den zwei Unbekannten $u_{1} und u_{2}$ zur Verfügung. Diese Gleichungen lassen sich nach $u_{1} und u_{2}$ auflösen und man erhält:

$\begin{array}{l} u_{1} = \frac{2 m_{2} \cdot v_{2} + (m_{1} - m_{2}) v_{1}}{m_{1} + m_{2}} \\ und \\ u_{2} = \frac{2 m_{1} \cdot v_{1} + (m_{2} - m_{1}) v_{2}}{m_{1} + m_{2}} \end{array}$

Ein wichtiger Spezialfall ist der, dass ein Körper elastisch gegen einen zweiten mit sehr großer Masse (feste Wand) stößt. Unter der Bedingung

$\begin{array}{l} m_{2} > > m_{1} und v_{2} = 0 erhält man: \\ u_{1} = - v_{1} \\ u_{2} = 0 \end{array}$

Das bedeutet: Der leichtere Körper wird an der festen Wand reflektiert. Er behält den Betrag seiner Geschwindigkeit bei. Die Richtung der Geschwindigkeit kehrt sich um.

Hinweis:

Die Umstellung der Gleichungen ist relativ aufwändig. Ein möglicher Weg wäre folgender:
Die Gleichung (2) für die Energie wird umgeschrieben. Die Multiplikation mit dem Faktor 2 ergibt:

$m_{1} \cdot v_{1}^{2} + m_{2} \cdot v_{2}^{2} = m_{1} \cdot u_{1}^{2} + m_{2} \cdot u_{2}^{2}$

Dafür kann man auch schreiben:

$\begin{array}{l} m_{1} \cdot (v_{1}^{2} - u_{1}^{2}) = m_{2} \cdot (u_{2}^{2} - v_{2}^{2}) \\ Unter Anwendung einer binomischen Formel \\ erhält man: \\ m_{1} \cdot (v_{1} - u_{1}) \cdot (v_{1} + u_{1}) = m_{2} \cdot (u_{2} - v_{2}) \cdot (u_{2} + v_{2}) (3) \end{array}$

Diese Gleichung wird dividiert durch die Impulsgleichung (1), die aber in folgende Form umgestellt wird:

$m_{1} \cdot (v_{1} - u_{1}) = m_{2} \cdot (u_{2} - v_{2}) (4)$

Die Division von Gleichung (3) durch Gleichung (4) ergibt:

$\begin{array}{l} v_{1} + u_{1} = u_{2} + v_{2} \\ Diese Gleichung wird nach u_{2} umgestellt: \\ u_{2} = v_{1} + u_{1} - v_{2} (5) \\ Setzt man die Gleichung (5) in die Impulsgleichung (1) ein, \\ so erhält man: \\ m_{1} \cdot v_{1} + m_{2} \cdot v_{2} = m_{1} \cdot u_{1} + m_{2} (v_{1} + u_{1} - v_{2}) \\ Diese Gleichung wird schließlich schrittweise nach u_{1} umgestellt: \\ m_{1} \cdot u_{1} + m_{2} \cdot u_{2} = m_{1} \cdot v_{1} + m_{2} \cdot v_{2} - m_{2} \cdot v_{1} + m_{2} \cdot v_{2} \\ u_{1} (m_{1} + m_{2}) = 2 m_{2} \cdot v_{2} + (m_{1} - m_{2}) \cdot v_{1} \\ u_{1} = \frac{2 m_{2} \cdot v_{2} + (m_{1} - m_{2}) \cdot v_{1}}{m_{1} + m_{2}} \end{array}$

Die entsprechende Gleichung für $u_{2}$ erhält man in analoger Weise, indem man von Gleichung (5) ausgeht, diese nach $u_{1}$ umstellt, in die Impulsgleichung einsetzt und die Gleichung nach dem obigen Muster umstellt.

Ein klassisches Experiment zum elastischen Stoß

Bild 4 zeigt ein klassisches Experiment zur Energieerhaltung und Impulserhaltung beim elastischen Stoß, das als „Newtons Wiege“ bezeichnet wird. Das entsprechende Gerät nennt man auch Kugelstoßapparat. Lässt man eine Kugel stoßen, dann fliegt auf der anderen Seite genau eine Kugel weg. Bei zwei stoßenden Kugeln sind es auf der anderen Seite genau zwei Kugeln usw.
Die Erklärung dafür ist folgende: Die Anzahl i Kugeln (i = 1, 2, ...) der Masse m wurden ausgelenkt und stoßen mit der Geschwindigkeit v auf die verbliebenen Kugeln. Nach dem Stoß fliegen k Kugeln mit der Geschwindigkeit u nach rechts fort. Nach dem Impulserhaltungssatz und dem Energieerhaltungssatz gilt dann:

$\begin{array}{l} i \cdot m \cdot v = k \cdot m \cdot u \\ und \\ i \frac{1}{2} m \cdot v^{2} = k \frac{1}{2} m \cdot u^{2} \end{array}$

Setzt man die erste Gleichung in die zweite ein, folgt i = k und daraus v = u, also genau das, was man sieht.

Lernhelfer (Duden Learnattack GmbH): "Zentraler gerader elastischer Stoß." In: Lernhelfer (Duden Learnattack GmbH). URL: http://www.lernhelfer.de/index.php/schuelerlexikon/physik-abitur/artikel/zentraler-gerader-elastischer-stoss (Abgerufen: 21. May 2025, 01:45 UTC)

Suche nach passenden Schlagwörtern

Jetzt durchstarten

Entspannt durch die Schule mit KI-Tutor Kim und Duden Learnattack.

Kim hat in Deutsch, Mathe, Englisch und 6 weiteren Schulfächern immer eine von Lehrkräften geprüfte Erklärung, Video oder Übung parat.
24/7 auf Learnattack.de und WhatsApp mit Bildupload und Sprachnachrichten verfügbar. Ideal, um bei den Hausaufgaben und beim Lernen von Fremdsprachen zu unterstützen.
Viel günstiger als andere Nachhilfe und schützt deine Daten.