Auftrieb in strömenden Flüssigkeiten und Gasen

Das Fliegen von Flugzeugen oder von Vögeln beruht darauf, dass es durch die Bewegung des Körpers gegenüber der Luft (Relativbewegung) eine nach oben gerichtete Auftriebskraft gibt. Sie wirkt der Gewichtskraft entgegen. Allgemein gilt:

Wird ein Körper von einer Flüssigkeit oder einem Gas umströmt, so kann eine in der Regel nach oben gerichtete Kraft auftreten. Diese Erscheinung wird als dynamischer Auftrieb, die dadurch wirkende Kraft als Auftriebskraft bezeichnet.

Entscheidend für das Auftreten des dynamischen Auftriebes sind zwei Faktoren:

1. Es muss eine Relativbewegung zwischen einem Körper und einer Flüssigkeit bzw. einem Gas vorhanden sein. Dabei ist es egal, ob sich der Körper in dem Stoff (Flüssigkeit, Gas) oder der Stoff um den Körper bewegt. Entscheidend für die Größe des Auftriebes ist die Relativgeschwindigkeit.
2. Ein dynamischer Auftrieb entsteht vor allem bei der Bewegung von Körpern mit einem Tragflächenprofil, wie es die Tragflächen von Flugzeugen und die Flügel von Vögeln aufweisen.

Ursachen für den dynamischen Auftrieb

Ursachen für den dynamischen Auftrieb sind zwei Effekte, die in Abhängigkeit von der Körperform und vom Anstellwinkel unterschiedliche Bedeutung haben.

1. Die Strömung wird durch den Körper aufgeteilt. Durch die Form des Körpers wird z. B. Luft vom Körper nach unten abgelenkt. Damit entsteht eine nach oben wirkende Kraft. Besonders deutlich ist dieser Effekt beispielsweise, wenn eine schräg stehende Platte von einem Luftstrom angeströmt wird. Auch bei Drachen spielt dieser Effekt eine entscheidende Rolle.
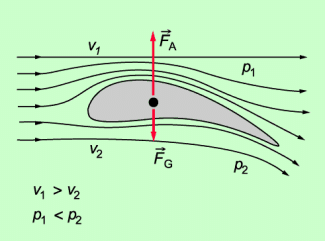
2. Durch die Aufteilung der Strömung und das Tagflächenprofil (Bild 2) entsteht oberhalb der Tragfläche ein Bereich mit größerer Strömungsgeschwindigkeit und nach den bernoullischen Gesetz demzufolge mit kleinerem Druck als unterhalb der Tragfläche. Der Druckunterschied zwischen Oberseite und Unterseite führt zu einer Auftriebskraft nach oben.

Wie groß die Auftriebskraft an einer Tragfläche ist, hängt bei einer Fläche mit bestimmtem Profil ab

• vom Anstellwinkel der Tragfläche gegenüber der Strömungsrichtung und
• von der Strömungsgeschwindigkeit
  (Relativgeschwindigkeit zwischen Tragfläche und Luft).

Nutzung des dynamischen Auftriebs

Der dynamische Auftrieb wird von Vögeln und bei Flugzeugen genutzt. Genauere Informationen zu Flugzeugen sind in dem Thema „Flugzeuge - physikalisch betrachtet" zu finden.

Der dynamische Auftrieb wird auch bei Autos, insbesondere bei Sport- und Rennwagen, genutzt. Durch Spoiler und tragflächenähnliche Anordnungen kann erreicht werden, dass die durch die strömende Luft hervorgerufene Kraft nach unten wirkt und dadurch das Fahrzeug kräftiger gegen die Straße gepresst wird. Damit ist ein schnelleres Bremsen, Beschleunigen und Durchfahren von Kurven möglich.