Keplersche Gesetze

Der Astronom JOHANNES KEPLER (1571-1630) entdeckte die grundlegenden Gesetze der Planetenbewegung. Seine Erkenntnisse sind zusammengefasst in den nach ihm benannten drei keplerschen Gesetzen.

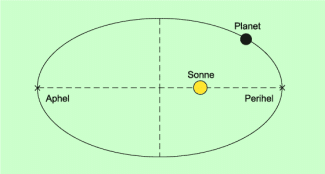
1. keplersches Gesetz: Das 1. keplersche Gesetz beschreibt die Bahnen, auf denen sich Planeten um die Sonne bewegen (Bild 1). Es lautet:

Die Planeten bewegen sich auf elliptischen Bahnen. In einem gemeinsamen Brennpunkt steht die Sonne.

Aus diesem Gesetz folgt, dass sich bei der Bewegung von Planeten um die Sonne der Abstand Planet-Sonne ständig ändert. So beträgt beispielsweise für die Erde der geringste Abstand von der Sonne 147,1 Mio. Kilometer (Perihel, Anfang Januar) und die größte Entfernung 152,1 Mio. Kilometer (Aphel, Anfang Juli). Die mittlere Entfernung der Erde von der Sonne hat einen Wert von 149,6 Mio. Kilometer. Diese Entfernung wird als Astronomische Einheit (Abkürzung: 1 AE) bezeichnet.

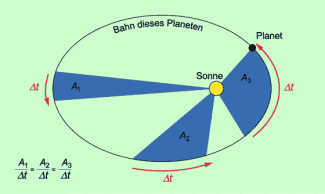
2. keplersches Gesetz: Das 2. keplersche Gesetz macht Aussagen über die Bewegung von Planeten längs ihrer Bahn. Es lautet:

Die Verbindungslinie Sonne-Planet überstreicht in gleichen Zeiten gleich große Flächen.

$\begin{array}{l}\frac{A_1}{\Delta t}=\frac{A_2}{\Delta t}=\frac{A_3}{\Delta t}=\text{konstant}\\ A\text{ Flächeninhalt}\\ \Delta t\text{ Zeitintervall}\\ \end{array}$

Aus diesem Gesetz folgt, das sich die Planeten auf ihrer Bahn mit unterschiedlicher Geschwindigkeit bewegen. In Sonnennähe sind sie schneller als in Sonnenferne. Für die Erde betragen diese Geschwindigkeiten 29,3 km/s in Sonnenferne (Juni/Juli) und 30,3 km/s in Sonnennähe (Dezember/Januar).

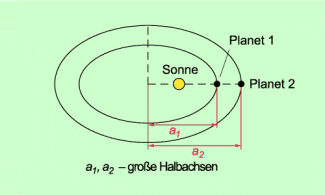
3. keplersches Gesetz: Das 3. keplersche Gesetz beschreibt den Zusammenhang zwischen der Größe der Bahn und der Zeit für einen Umlauf um die Sonne.
Es lautet:

Die Quadrate der Umlaufzeiten zweier Planeten verhalten sich wie die dritten Potenzen der großen Halbachsen ihrer Bahnen.

$\begin{array}{l}\frac{T_1^2}{T_2^2}=\frac{a_1^3}{a_2^3}\\ T_1,T_2\text{ Umlaufzeiten zweier Planeten}\\ a_1,a_2\text{ große Halbachsen der Bahnen}\end{array}$

Mithilfe dieses Gesetzes können aus den beobachtbaren Umlaufzeiten der Planeten um die Sonne die wahren Dimensionen des Planetensystems hergeleitet werden. Insbesondere folgt aus diesem Gesetz, dass die Bahngeschwindigkeit von Planeten mit wachsendem Abstand von der Sonne abnimmt. So bewegt sich z. B. Merkur als sonnennächster Planet schneller um die Sonne als die Erde. Die Erde bewegt sich ihrerseits schneller um die Sonne als die sonnenfernen Planeten Saturn oder Pluto.

Beachte: Die keplerschen Gesetze gelten nicht nur für die Bewegung von Planeten, sondern für alle Bewegungen von Himmelskörpern um einen Zentralkörper, also z.B. auch für die Bewegung eines künstlichen Satelliten um die Erde.