Bernoulli-Ketten und ihre Simulation

Eine n-fach und unabhängig voneinander ausgeführte Realisierung eines BERNOULLI-Experiments mit der Erfolgswahrscheinlichkeit p heißt BERNOULLI-Kette der Länge n und mit der Erfolgswahrscheinlichkeit p oder kurz BERNOULLI-Kette mit den Parametern n und p.

Dazu betrachten wir im Folgenden ein Anwendungsbeispiel.

Beispiel: Jeder der fünf Elfmeterspezialisten des Fußballvereins Rodatal verwandelt einen Elfmeter erfahrungsgemäß mit einer Wahrscheinlichkeit von 0,80. Beim Pokalausscheid mit dem Ortsrivalen kommt es zum Elfmeterschießen.
Mit welcher Wahrscheinlichkeit verwandeln die Rodataler genau vier ihrer fünf Elfmeter?

Um diese Frage zu beantworten, modellieren wir die fünf Elfmeterschüsse der Rodataler Fußballer durch eine BERNOULLI-Kette.

Das Elfmeterschießen der Rodataler Fußballer ist eine BERNOULLI-Kette der Länge 5 und mit der Erfolgswahrscheinlichkeit 0,80.

Dabei muss beachtet werden, dass sowohl die Unabhängigkeit der einzelnen „Schuss-Vorgänge“ als auch die gleichbleibende Erfolgswahrscheinlichkeit idealisierte Annahmen sind, wie es vielfach bei der Beschreibung realer Vorgänge durch eine BERNOULLI-Kette der Fall ist.

Eine BERNOULLI-Kette mit den Parametern n und p ist ein n-stufiges Zufallsexperiment. Sein Baumdiagramm weist auf jeder Stufe zwei Ergebnisse auf, nämlich Erfolg (1) und Misserfolg (0), wobei jede Übergangswahrscheinlichkeit zum Erfolg p beträgt und zum Misserfolg $1 - p$ .

Baumdiagramm einer Bernoulli-Kette

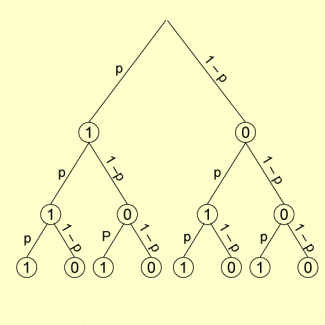
Dieses Zufallsexperiment besitzt also genau $2^{n}$ Ergebnisse. Jedes Ergebnis ist ein n-Tupel $(e_{1}; e_{2}; ...; e_{n})$ , wobei jede Koordinate entweder den Wert 1 oder den Wert 0 besitzt. Ein solches Ergebnis tritt mit folgender Wahrscheinlichkeit ein:
$P ({(e_{1}; e_{2}; ...; e_{n})}) = p^{A n z a h l d e r E r f o \lg e} \cdot {(1 - p)}^{A n z a h l d e r M i s s e r f o \lg e}$

Die Berechnung dieser Wahrscheinlichkeit erfordert keinen hohen Aufwand. Da die Erfolge jeweils mit 1 und die Misserfolge mit 0 bezeichnet sind, kann die Anzahl der Erfolge bzw. der Misserfolge jeweils als Summe der $e_{i}$ geschrieben werden. Man erhält:
$P ({(e_{1}; e_{2}; ...; e_{n})}) = p^{\sum_{i = 1}^{n} e_{i}} \cdot {(1 - p)}^{n - \sum_{i = 1}^{n} e_{i}}$

Hieraus ergibt sich, dass jedes atomare Ereignis ${(e_{1}; e_{2}; ...; e_{n})}$ mit derselben Anzahl k von Erfolgen die gleiche Wahrscheinlichkeit besitzt.

Da es genau
$(\begin{matrix} n \\ k \end{matrix})$
derartige Ergebnisse $(e_{1}; e_{2}; ...; e_{n})$ mit genau k Erfolgen gibt, berechnen sich die Wahrscheinlichkeiten der Anzahl von Erfolgen bei zusammengesetzten Ereignissen nach der sogenannten BERNOULLI-Formel:
$P ({g e n a u k E r f o \lg e i n d e r B E R N O U L L I -Kette}) = (\begin{matrix} n \\ k \end{matrix}) \cdot p^{k} \cdot {(1 - p)}^{n - k}$

Anmerkung: Der Binomialkoeffizient
$(\begin{matrix} n \\ k \end{matrix})$
wird durch das Zählprinzip für Mengen geliefert.

Mit der BERNOULLI-Formel kann jetzt auch die eingangs gestellte Frage beantwortet werden. Es ist:
$\begin{array}{l} P ({g e n a u 4 d e r 5 E l f m e t e r s c h ü s s e v e r w a n d e \ln d i e R o d a t a l e r}) \\ = (\begin{matrix} 5 \\ 4 \end{matrix}) \cdot {0,80}^{4} \cdot {(1 - 0,80)}^{5 - 4} \approx 0,41 \end{array}$

Zur Simulation einer BERNOULLI-Kette der Länge n und mit der Erfolgswahrscheinlichkeit p lässt sich die auf dem TI-92 zu programmierende Funktion simbin nutzen.

Programm zur Simulation einer Bernoulli-Kette

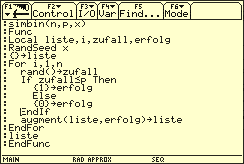
Gibt man im HOME-Editor zum Beispiel $simbin (5, 0.8, 32456)$ ein, so wird auf dem Bildschirm eine Liste der Länge $n = 5$ angezeigt, in der 1 für Erfolg und 0 für Misserfolg steht.

(Die zusätzliche Eingabe eines sich von Simulation zu Simulation ändernden, aber ansonsten beliebigen x-Wertes dient der Initialisierung des Zufallsgenerators. Verändert man den x-Wert nicht, so werden dieselben Listen erstellt.)

Die angezeigte Liste stellt zugleich eine Simulation der fünf Elfmeterschüsse der Rodataler Sportler dar.

Mit der Funktion $simbin (5, 0.7, 491156)$ könnten die fünf Elfmeterschüsse der gegnerischen Mannschaft simuliert werden, wenn deren Elfmeterschützen erfahrungsgemäß eine Erfolgswahrscheinlichkeit von jeweils 0,70 haben. Zählt man die entsprechenden Treffer (Einsen) aus, kann festgestellt werden, welche der beiden Mannschaften das „Elfmeterschießen“ gewonnen hat.

Anregung: Diese Prozedur könnte man 100-mal wiederholen und zum Beispiel untersuchen, wie oft die Rodataler Fußballer als die besseren Elfmeterschützen diese Art des Elfmeterschießens verlieren.

Stand: 2010
Dieser Text befindet sich in redaktioneller Bearbeitung.

Mathe Note verbessern?

Kostenlos bei Duden Learnattack registrieren und ALLES 48 Stunden testen.

Kein Vertrag. Keine Kosten.

40.000 Lern-Inhalte in Mathe, Deutsch und 7 weiteren Fächern
Hausaufgabenhilfe per WhatsApp
Original Klassenarbeiten mit Lösungen
Deine eigene Lern-Statistik
Kostenfreie Basismitgliedschaft

Mathe kostenlos lernen

Verwandte Artikel

Bernoulli-Ketten und ihre Simulation

Rechtliches

Einloggen