Ebenenbüschel im Raum
- Definition: Die Menge der Ebenen des Raumes, die eine feste Gerade enthalten, heißt Ebenenbüschel.
-
Ebenenbüschel
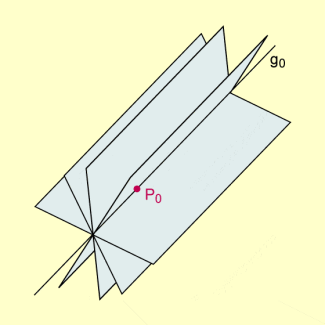
-
Schnittgerade zweier Ebenen eines Büschels
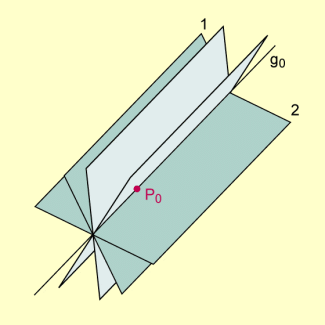
Da die Gerade schon als Schnittgerade von zwei Ebenen des Büschels eindeutig bestimmt ist, kann man sagen, dass jedes Ebenenbüschel im Raum durch zwei seiner Ebenen eindeutig bestimmt ist.
Allgemeiner lässt sich sogar feststellen, dass zwei nicht zueinander parallele Ebenen im Raum ein Ebenenbüschel eindeutig bestimmen, da diese beiden Ebenen einander stets in einer Geraden schneiden.
Um eine analytische Beschreibung eines Ebenenbüschels zu gewinnen, werden zwei voneinander verschiedene Ebenen betrachtet, die beide die Gerade enthalten. Jede dieser beiden Ebenen lässt sich z.B. durch den Ortsvektor zu einem Stützpunkt von und einen zugehörigen Normalenvektor beschreiben.
-
Normalenvektoren zweier Ebenen eines Büschels
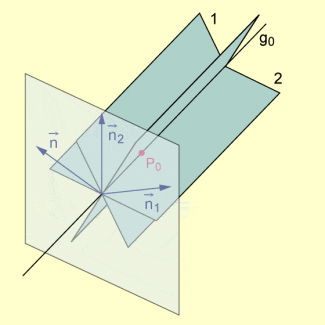
Es ist dann
Jede andere Ebene , die enthält, enthält auch und kann ebenfalls durch den Ortsvektor zu und einen Normalenvektor beschrieben werden. Es gilt dann:
Weil nicht parallel zueinander sind, sind auch nicht parallel zueinander, d.h., die beiden Normalenvektoren sind linear unabhängig voneinander.
Darüber hinaus sind die Vektoren jeweils senkrecht zu und liegen folglich in einer (zu senkrechten) gemeinsamen Ebene. Damit lässt sich der Vektor als Linearkombination von auffassen:
Unter Verwendung dieses Resultats erhält man aus der obigen Gleichung von :
Damit lässt sich das durch bestimmte Ebenenbüschel im Raum und damit jede Ebene, die enthält, als eine Linearkombination der Gleichungen von zwei Ebenen des Büschels auffassen.
- Satz: Sind zwei voneinander verschiedene Ebenen, die die Gerade mit dem Stützpunkt enthalten, so beschreibt
das zu gehörende Ebenenbüschel.
Kennzeichnet man die beiden zueinander nicht parallelen Ebenen durch ihre Gleichungen in allgemeiner Form, also
so beschreibt in analoger Weise![]()
das durch bestimmte Ebenenbüschel.
Damit kann man bei geeigneter Wahl von p und q mit
die Gleichung jeder Ebene beschreiben, die die Schnittgerade von mit dem Stützpunkt enthält.

