Geradenbündel im Raum

• Definition: Die Menge der Geraden des Raumes, die durch einen festen Punkt $P_0$ gehen, heißt Geradenbündel im Raum.

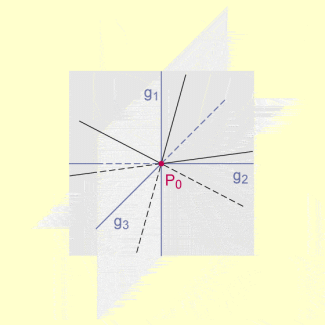
Im Unterschied zu einem Geradenbüschel, einem Ebenenbüschel oder einem Ebenenbündel lässt sich ein Geradenbündel im Raum analytisch nicht als Linearkombination der Gleichungen von Geraden des Bündels durch $P_0$ beschreiben.

Ein Grund hierfür ist, dass sich Geraden im Raum analytisch nicht durch einen Punkt $P_0$ und einen Normalenvektor eindeutig beschreiben lassen.

Eine analytische Beschreibung von Geraden im Raum ist aber z. B. durch eine Punktrichtungsgleichung in vektorieller Schreibweise möglich:
$g:\overrightarrow{x}={\overrightarrow{p}}_0+t\overrightarrow{a}$

Betrachten wir nun die Gleichungen von zwei voneinander verschiedenen Geraden $g_{1}und{g}_2$ des Raumes, die durch $P_0$ gehen. Gilt
$g_1:\overrightarrow{x}={\overrightarrow{p}}_0+t{\overrightarrow{a}}_{1}und{g}_2:\overrightarrow{x}={\overrightarrow{p}}_0+t{\overrightarrow{a}}_2,$

so beschreibt
$g:\overrightarrow{x}={\overrightarrow{p}}_0+t\left(p{\overrightarrow{a}}_1+q{\overrightarrow{a}}_2\right),p,q\in ℝ,p,qnichtgleichzeitig0;t\in ℝ$
alle Geraden durch $P_0$, die in der von $g_{1}und{g}_2$ aufgespannten Ebene liegen.

Nimmt man noch eine dritte Gerade $g_3:\overrightarrow{x}={\overrightarrow{p}}_0+t{\overrightarrow{a}}_3$ hinzu, die durch $P_0$ geht und die nicht in der von $g_{1}und{g}_2$ aufgespannten Ebene liegt, so ist $\{{\overrightarrow{a}}_1,{\overrightarrow{a}}_2,{\overrightarrow{a}}_3\}$ ein System linear unabhängiger Vektoren.

Damit beschreibt aber
$\begin{array}{l} g:\overrightarrow{x}={\overrightarrow{p}}_0+t\left(p{\overrightarrow{a}}_1+q{\overrightarrow{a}}_2+r{\overrightarrow{a}}_3\right),\\ (p,q,r\in R,p,q,rnichtgleichzeitig0;t\in R) \end{array}$
jede Gerade des Raumes durch $P_0$ und damit auch das Geradenbündel durch $P_0$.

• Satz: Ist $\{{\overrightarrow{a}}_1,{\overrightarrow{a}}_2,{\overrightarrow{a}}_3\}$ ein System linear unabhängiger Richtungsvektoren von drei Geraden eines Bündels, so beschreibt
  $\begin{array}{l}g:\overrightarrow{x}={\overrightarrow{p}}_0+t\left(p{\overrightarrow{a}}_1+q{\overrightarrow{a}}_2+r{\overrightarrow{a}}_3\right),\\ (p,q,r\in R,p,q,rnichtgleichzeitig0;t\in R)\end{array}$
  jede Gerade des Raumes $P_0$ durch und damit auch das Geradenbündel durch $P_0$.