Histogramme

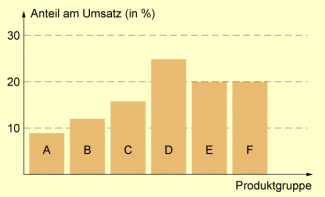
Die Säulenbreite, d.h. die Breite $b_i$ des Rechtecks über der Klasse $K_i$ bzw. über $x_i$, ist frei wählbar, wobei sich die einzelnen Säulen allerdings nicht überschneiden dürfen.

Für die beschreibende Statistik wählt man $b_i$ meist so, dass ein möglichst geschlossenes und damit optisch ansprechendes Säulenbild entsteht.

Das hat allerdings zur Folge, dass auf der Ordinatenachse als Rechteckhöhe
$\frac{h_n\left(K_i\right)}{b_i}$ bzw. $\frac{P\left(X=x_i\right)}{b_i}$
abgetragen werden muss.

Dieser Sachverhalt wird in populärwissenschaftlichen oder journalistischen Darstellungen verschiedentlich nicht berücksichtigt.

In der Wahrscheinlichkeitstheorie wählt man in der Regel einheitlich die (Säulen-)Breite 1, weil dadurch die Rechteckhöhe gleich $P\left(X=x_i\right)$ ist, sodass die entsprechende Einzelwahrscheinlichkeit direkt abgelesen werden kann.

Entscheidend ist aber nur, dass die Rechtecke eines Histogramms jeweils den Flächeninhalt $h_n\left(K_i\right)$ bzw. $P\left(X=x_i\right)$ aufweisen.

• Beispiel:
  $X\stackrel{\wedge}{=}\left(\begin{array}{ccccccc}-8& -4& -2& 2& 4& 6& 8\\ \frac{3}{36}& \frac{1}{36}& \frac{14}{36}& \frac{7}{36}& \frac{8}{36}& \frac{1}{36}& \frac{2}{36}\end{array}\right)$

Das zugehörige Histogramm mit der Rechteckbreite 1 ist aufgrund seiner „Zerklüftetheit“ optisch wenig ansprechend (in der folgenden Abbildung links). Wählt man einheitlich die Rechteckbreite 2, so macht das zugehörige Histogramm einen geschlosseneren Eindruck (in der folgenden Abbildung rechts).

Mit dem Programm drawhist(mat) können außerdem durch Eingabe einer frei wählbaren zweizeiligen Matrix interaktiv Histogramme erzeugt werden.