Monotonie und Beschränktheit von Zahlenfolgen

Eine Zahlenfolge $(a_{n})$ heißt genau dann monoton wachsend bzw. monoton fallend, wenn für alle $n \in ℕ$ gilt:
$a_{n + 1} \geq a_{n} b z w . a_{n + 1} \leq a_{n}$
Wenn jedes Folgenglied echt größer (kleiner) als sein Vorgänger ist, so spricht man von streng monoton wachsenden (fallenden) Folgen.
Eine Zahlenfolge $(a_{n})$ heißt genau dann nach oben beschränkt bzw. nach unten beschränkt, wenn es eine Zahl $s \in ℝ$ gibt, so dass für alle Folgenglieder $a_{n}$ gilt:
$a_{n} \leq s b z w . a_{n} \geq s$
Man nennt die reelle Zahl s dann eine obere bzw. eine untere Schranke der Zahlenfolge $(a_{n})$ .

Annäherung

Wir betrachten die Zahlenfolgen, die sich aus den nachstehend dargestellten Vorgängen bzw. Situationen ergeben:

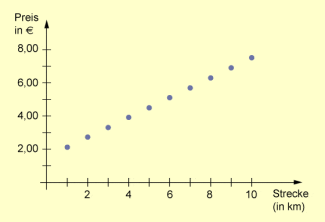
(1) Für die Fahrt mit einem Taxi in A-Stadt sind ein Grundpreis von 1,50 Euro und für jeden Kilometer zusätzlich 0,60 Euro zu zahlen.
Der Fahrpreis bei einer Fahrt von 1 km, 2 km, 3 km, ..., 10 km Länge beträgt demzufolge 2,10 Euro, 2,70 Euro, 3,30 Euro, ..., 7,50 Euro.

Beispiel einer streng monoton wachsenden Zahlenfolge

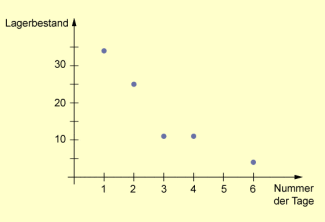
(2) Eine Buchhandlung hat 200 Exemplare eines bestimmten Buches auf Lager. Im Verlaufe einer Woche werden davon am ersten Tag 34 Bücher, am zweiten Tag 25 Bücher, am dritten und vierten Tag jeweils 11 Bücher, am fünften Tag kein Buch und am sechsten Tag 4 Bücher verkauft.
Der Lagerbestand an Büchern beträgt im Verlauf der Woche: 200; 166; 141; 130; 119; 119; 115.

Beispiel einer monoton fallenden Zahlenfolge

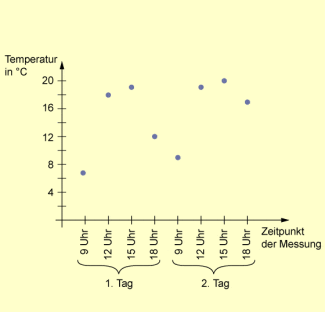
(3) Schüler nehmen an zwei Tagen jeweils um 9 Uhr; 12 Uhr, 15 Uhr und 18 Uhr ein Messung der Lufttemperatur vor. Sie erhalten folgende Werte (in $° C$ ): 7; 18; 19; 12; 9; 19; 20; 17.

Beispiel einer Zahlenfolge, die weder monoton wachsend noch monoton fallend ist

Vergleicht man die Zahlenwerte in diesen drei Beispielen, so kann man feststellen, dass in (1) die Glieder der Preisfolge ständig zunehmen, in (2) der Lagerbestand sich von Tag zu Tag verringert oder mindestens gleich bleibt, in (3) jedoch keine solcher Regelmäßigkeiten auftritt.

Definitionen

Dies führt zu folgenden Begriffsbildungen (Definitionen):

Eine Zahlenfolge $(a_{n})$ heißt genau dann monoton wachsend , wenn für alle $n \in ℕ$ gilt:
$a_{n + 1} \geq a_{n}$ bzw. $a_{n + 1} - a_{n} \geq 0$
Eine Zahlenfolge $(a_{n})$ heißt genau dann monoton fallend , wenn für alle $n \in ℕ$ gilt:
$a_{n + 1} \leq a_{n}$ bzw. $a_{n + 1} - a_{n} \leq 0$

Bei monoton wachsenden oder monoton fallenden Folgen können aufeinander folgende Folgenglieder gleich sein.
Wenn jedes Folgenglied echt größer (kleiner) als sein Vorgänger ist, so spricht man von streng monoton wachsenden (fallenden) Folgen.
Konstante Zahlenfolgen wie z.B. $(a_{n}) = 3; 3; 3; ...$ oder $(a_{n}) = (\frac{1^{n}}{2}) = \frac{1}{2}; \frac{1}{2}; \frac{1}{2}; ...$ sind sowohl monoton wachsend oder als auch monoton fallend, denn mit $a_{n + 1} = a_{n}$ gilt auch $a_{n + 1} \geq a_{n}$ und $a_{n + 1} \leq a_{n}$ .

Beispiel 1

Es ist das Monotonieverhalten der Zahlenfolge $(a_{n}) = (\frac{n}{n + 1})$ zu untersuchen.

Wir betrachten hierzu die Differenz $a_{n + 1} - a_{n}$ .
Es gilt im vorliegenden Fall:
$\begin{matrix} a_{n + 1} - a_{n} = \frac{n + 1}{n + 2} - \frac{n}{n + 1} \\ = \frac{{(n + 1)}^{2} - n (n + 2)}{(n + 2) (n + 1)} = \frac{1}{(n + 2) (n + 1)} \end{matrix}$

Der als Resultat erhaltene Bruch ist stets positiv, da Zähler und Nenner positiv sind.
Wegen $a_{n + 1} - a_{n} > 0$ ist die Folge also streng monoton wachsend.

Beispiel 2

Die Zahlenfolge $(a_{n}) = ({(- 1)}^{n} \cdot n)$ ist auf Monotonie zu untersuchen.

Die Anfangsglieder der Folge lauten $- 1; 2; - 3; 4; - 5; 6; ...$ .
Bereits hieraus kann man entnehmen, dass die Folge wegen $a_{1} < a_{2}$ , aber $a_{2} > a_{3}$ nicht monoton sein kann - es handelt sich hier (wegen des Vorzeichenwechsels von Glied zu Glied) um eine alternierende Zahlenfolge.

Die rechnerische Überprüfung ergibt in diesem Fall:
$\begin{matrix} a_{n + 1} - a_{n} = {(- 1)}^{n + 1} \cdot (n + 1) - {(- 1)}^{n} \cdot n \\ = {(- 1)}^{n} [(- n - 1) - n] = - {(- 1)}^{n} (2 n + 1) \end{matrix}$

Diese Differenz ist aber in Abhängigkeit davon, ob n gerade oder ungerade ist, jeweils negativ oder positiv. Die Folge ist also nicht monoton.

Weitere Definitionen

Eine Zahlenfolge $(a_{n})$ heißt genau dann nach oben beschränkt, wenn es eine reelle Zahl $s \in ℝ$ gibt, sodass für alle Folgeglieder $a_{n}$ gilt:
$a_{n} \leq s$
Man nennt die reelle Zahl s dann eine obere Schranke der Zahlenfolge $(a_{n})$ .
Eine Zahlenfolge $(a_{n})$ heißt genau dann nach unten beschränkt, wenn es eine reelle Zahl $s \in ℝ$ gibt, so dass für alle Folgeglieder $a_{n}$ gilt:
$a_{n} \geq s$
Man nennt die reelle Zahl s dann eine untere Schranke der Zahlenfolge $(a_{n})$ .

Anmerkung: Einfach von „Schranke“ spricht man, wenn $| a_{n} | \leq s$ , also wenn alle $a_{n}$ in dem Intervall $[- s; s]$ liegen.

Eine Zahlenfolge $(a_{n})$ heißt genau dann beschränkt, wenn sie eine obere und eine untere Schranke besitzt.

Beispiel 3

Die Folge $(a_{n}) = (\frac{n}{n + 1})$ ist auf Beschränktheit zu untersuchen.

Wegen $(a_{n}) = \frac{1}{2}; \frac{2}{3}; \frac{3}{4}; \frac{4}{5}; ...$ kann man vermuten, dass $s = 1$ eine obere Schranke von $(a_{n})$ ist.
Um dies nachzuweisen, muss man zeigen, dass $a_{n} - s \leq 0$ für alle n gilt. Dies trifft zu, denn
$\frac{n}{n + 1} - 1 = \frac{n - (n + 1)}{n + 1} = \frac{- 1}{n + 1} < 0$
(der Zähler ist negativ und der Nenner für alle n positiv).

Stand: 2010
Dieser Text befindet sich in redaktioneller Bearbeitung.

Mathe Note verbessern?

Kostenlos bei Duden Learnattack registrieren und ALLES 48 Stunden testen.

Kein Vertrag. Keine Kosten.

40.000 Lern-Inhalte in Mathe, Deutsch und 7 weiteren Fächern
Hausaufgabenhilfe per WhatsApp
Original Klassenarbeiten mit Lösungen
Deine eigene Lern-Statistik
Kostenfreie Basismitgliedschaft

Mathe kostenlos lernen

Verwandte Artikel