Satz des Menelaos
Der nach MENELAOS VON ALEXANDRIA (um 100) benannte Satz macht eine Aussage über eine Eigenschaft einer Geraden, die die Seiten eines Dreiecks oder deren Verlängerungen schneidet. Ein Beweis des Satzes kann mithilfe der Strahlensätze erfolgen.
MENELAOS (auch MENELAUS) VON ALEXANDRIA lebte um 100 in Alexandria. Er ist heute vor allem durch den nach ihm benannten Satz über eine Eigenschaft einer Geraden, welche die Seiten eines Dreiecks schneidet, bekannt. Er hat aber auch drei Bücher geometrischen Inhalts (die „Sphaerica“) hinterlassen, in denen er vor allem Probleme der sphärischen Geometrie behandelt. Darin wurde der im Folgenden angeführte Satz auf den Fall verallgemeinert, dass ein sphärisches Dreieck von einem Großkreis geschnitten wird.
-
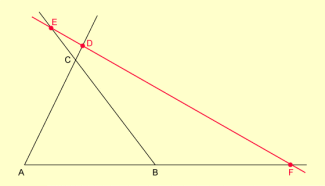
Figur zum Satz des Menelaos (Fall 1)
Eine Gerade, die nicht durch einen Eckpunkt eines Dreiecks geht und nicht zu einer der Dreiecksseiten parallel ist, schneidet entweder zwei Seiten des Dreiecks und die Verlängerung der dritten Seite (siehe Figur zum Satz des Menelaos (Fall 1)) oder die Verlängerungen aller Seiten (siehe Figur zum Satz des Menelaos (Fall 2)).
Die Strecken und heißen Abschnitte der Seiten. Die Strecken und sowie und sind nicht aneinander stoßende Abschnitte der Dreiecksseiten.
Über diese Figur macht der Satz des MENELAOS die im Folgenden angeführte Aussage.
- Schneidet eine Gerade die Seiten eines Dreiecks oder deren Verlängerungen, so sind die Produkte aus den Längen von je drei nicht aneinander stoßenden Abschnitten der Seiten gleich, d.h., es gilt:
Dividiert man diese Produktgleichung durch die Faktoren der rechten Seite, so ergibt sich als äquivalente Aussage die nachstehende.
- Schneidet eine Gerade die Seiten eines Dreiecks oder deren Verlängerungen, so ist das Produkt aus den Quotienten der Längen der auf den Seiten erzeugten Abschnitte gleich 1, d.h., es gilt:
Zu einem Beweis des Satzes kann die Vorüberlegung führen, dass aus der Produktgleichung Quotientengleichungen hergestellt werden können, in denen z.B. die Strecken und vorkommen. Dies wiederum verweist auf die Strahlensätze als „Lieferanten“ solcher Verhältnisse.
Um einen Strahlensatz anwenden zu können, muss die MENELAOS-Figur durch eine Hilfslinie so angereichert werden, dass parallele Strecken entstehen. Dazu benutzt man eine Parallele zu durch B, die die MENELAOS-Gerade in G schneidet (s. folgende Abbildung).
![]()
Dann gilt:
In beiden Quotientengleichungen kommt das Hilfsglied vor, das eliminiert werden kann. Man erhält
aus (1) bzw. aus (2)
und nach Gleichsetzen der rechten Seiten
.
Durch Multiplikation mit ergibt sich schließlich:
Ohne Beweis wird mitgeteilt, dass auch die Umkehrung des Satzes des MENELAOS wieder eine wahre Aussage ist.
- Bestimmen drei Punkte auf zwei Seiten eines Dreiecks und der Verlängerung der dritten bzw. auf den Verlängerungen aller drei Seiten solche Abschnitte, dass die Produkte der Längen von je drei nicht aneinander anstoßenden Abschnitten gleich sind, so liegen die drei Punkte auf einer Geraden.
Diese Umkehrung kann also dazu dienen, die Kollinearität dreier Punkte nachzuweisen.
-
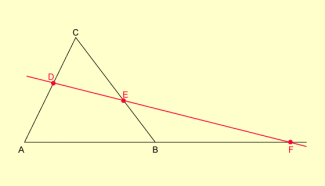
Figur zum Satz des Menelaos (Fall 2)