Schwerpunkt eines Dreiecks

Der Schwerpunkt S des Dreiecks $P_{1} P_{2} P_{3}$ ist der Schnittpunkt der Seitenhalbierenden. Er teilt diese (vom jeweiligen Eckpunkt des Dreiecks her gesehen) im Verhältnis $2 : 1.$
Im Folgenden sollen die Koordinaten des Schwerpunktes $S (x_{S}; y_{S}; z_{S})$ eines Dreiecks $P_{1} P_{2} P_{3}$ bestimmt werden.

Zunächst machen wir eine Vorbemerkung zur Teilung einer Strecke $\bar{P_{1} P_{2}}$ mit T als Teilpunkt. Es sei $\bar{P_{1} T} : \bar{T P_{2}} = λ$ das Verhältnis der Streckenteile.

Bild

Für das Teilverhältnis $λ$ gilt dann:

$λ > 0$ :
T ist innerer Teilungspunkt (T liegt zwischen $P_{1} u n d P_{2}$ ).
$λ < 0$ :
T ist äußerer Teilungspunkt.
$λ = 1$ :
T halbiert die (ist Mittelpunkt der) Strecke $\bar{P_{1} P_{2}}$ .

Allgemein gilt in der xy-Ebene für die Koordinaten eines Teilpunktes $T (x_{T}; y_{T})$ einer Strecke $\bar{P_{1} P_{2}}$ mit $P_{1} (x_{1}; y_{1})$ und $P_{2} (x_{2}; y_{2})$ :
$x_{T} = \frac{x_{1} + λ x_{2}}{1 + λ}; y_{T} = \frac{y_{1} + λ y_{2}}{1 + λ}$

Schwerpunkt eines Dreiecks in Koordinatendarstellung

Gegeben sei in der xy-Ebene ein Dreieck durch die Koordinaten seiner Eckpunkte $P_{1}, P_{2} u n d P_{3}$ .

Schwerpunkt eines Dreiecks (Koordinatendarstellung)

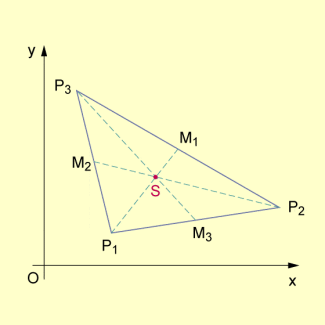
Unter Verwendung von $M_{1}$ als Mittelpunkt der Strecke $\bar{P_{2} P_{3}}$ lassen sich die Koordinaten des Schwerpunktes $S (x_{S}; y_{S})$ folgendermaßen angeben:
$x_{S} = \frac{x_{1} + 2 x_{M_{1}}}{3}; y_{S} = \frac{y_{1} + 2 x_{M_{1}}}{3}$

$M_{1}$ hat die Koordinaten $x_{M_{1}} = \frac{x_{2} + x_{3}}{2}$ und $y_{M_{1}} = \frac{y_{2} + y_{3}}{2} .$

In die Koordinaten von S eingesetzt liefert das die folgenden Werte für den Schwerpunkt $S (x_{S}; y_{S})$ :
$x_{S} = \frac{x_{1} + x_{2} + x_{3}}{3}; y_{S} = \frac{y_{1} + y_{2} + y_{3}}{3}$

Für den dreidimensionalen Fall lassen sich die Überlegungen analog führen, und für den Schwerpunkt $S (x_{S}; y_{S}; z_{S})$ gilt:
$x_{S} = \frac{x_{1} + x_{2} + x_{3}}{3}; y_{S} = \frac{y_{1} + y_{2} + y_{3}}{3}; z_{S} = \frac{z_{1} + z_{2} + z_{3}}{3}$

Beipiel 1: Es sind die Koordinaten des Schwerpunktes S des Dreiecks $P_{1} P_{2} P_{3}$ mit den Punkten $P_{1} (2; 1; 0), P_{2} (1; 0; 1), P_{3} (0; 1; 3)$ zu ermitteln.

Nach oben angegebener Formel ist:
$\begin{array}{l} x_{S} = \frac{2 + 1 + 0}{3} = 1; y_{S} = \frac{1 + 0 + 1}{3} = \frac{2}{3}; z_{S} = \frac{0 + 1 + 3}{3} = \frac{4}{3} \\ \Rightarrow S (1; \frac{2}{3}; \frac{4}{3}) \end{array}$

Schwerpunkt in Vektordarstellung

Es seien $\vec{p_{1}}, \vec{p_{2}} u n d \vec{p_{3}}$ die Ortsvektoren der Eckpunkte des Dreiecks $P_{1} P_{2} P_{3}$ , $\vec{t_{3}}$ der Ortsvektor von $T_{3}$ (Halbierungspunkt von $\bar{P_{1} P_{2}}$ ) und $\vec{s}$ der Ortvektor des Schwerpunktes S.

Bild

Dann gilt , und wegen $\vec{t_{3}} = \frac{\vec{p_{1}} + \vec{p_{2}}}{2}$ erhält man:
$\vec{s} = \frac{\vec{p_{1}} + \vec{p_{2}} + \vec{p_{3}}}{3}$

Beispiel 2: Man ermittle den Ortsvektor des Schwerpunktes S vom Dreieck $P_{1} P_{2} P_{3}$ mit den Punkten $P_{1} (4; 2; - 5), P_{2} (3; - 1; 2) u n d P_{3} (2; 2; 0)$ .

Es ist:
$\vec{s} = \frac{1}{3} ((\begin{matrix} 4 \\ 2 \\ - 5 \end{matrix}) + (\begin{matrix} 3 \\ - 1 \\ 2 \end{matrix}) + (\begin{matrix} 2 \\ 2 \\ 0 \end{matrix})) = \frac{1}{3} (\begin{matrix} 9 \\ 3 \\ - 3 \end{matrix}) = (\begin{matrix} 3 \\ 1 \\ - 1 \end{matrix})$

Stand: 2010
Dieser Text befindet sich in redaktioneller Bearbeitung.

Mathe Note verbessern?

Kostenlos bei Duden Learnattack registrieren und ALLES 48 Stunden testen.

Kein Vertrag. Keine Kosten.

40.000 Lern-Inhalte in Mathe, Deutsch und 7 weiteren Fächern
Hausaufgabenhilfe per WhatsApp
Original Klassenarbeiten mit Lösungen
Deine eigene Lern-Statistik
Kostenfreie Basismitgliedschaft

Mathe kostenlos lernen

Schwerpunkt eines Dreiecks

Schwerpunkt eines Dreiecks in Koordinatendarstellung

Schwerpunkt in Vektordarstellung

Rechtliches

Einloggen