Iterationsverfahren
Unter Iteration versteht man ein Verfahren zur schrittweisen Annäherung an die Lösung einer Gleichung unter Anwendung eines sich wiederholenden Rechengangs. Das bedeutet, (wenn es möglich ist) aus einer Näherungslösung durch Anwenden eines Algorithmus zu einer besseren Näherungslösung zu kommen und die Lösung beliebig gut an die exakte Lösung heranzuführen. Man sagt dann, dass die Iteration konvergiert.
Unter Iteration versteht man ein Verfahren zur schrittweisen Annäherung an die Lösung einer Gleichung unter Anwendung eines sich wiederholenden Rechengangs.
Das bedeutet, (wenn es möglich ist) aus einer Näherungslösung durch Anwenden eines Algorithmus zu einer besseren Näherungslösung zu kommen und die Lösung beliebig gut an die exakte Lösung heranzuführen. Man sagt dann, dass die Iteration konvergiert.
Zu den Iterationsverfahren gehört z. B. das sogenannte Heron-Verfahren.
In einer in der praktischen Mathematik als allgemeines Iterationsverfahren bezeichneten Methode wird folgendermaßen vorgegangen:
Bestimmt werden sollen die Lösungen von G(x) = 0.
Man stellt nun diese Gleichung in die Form x = g(x) um und fasst die umgestellte Form als zwei Funktionen auf:
Gesucht sind dann die Schnittpunkte der zugehörigen Graphen. Die Abszissen der Schnittpunkte wären dann die Lösungen der ursprünglichen Gleichung.
Zwei Fälle sind für dieses Vorgehen interessant:
1. Fall:
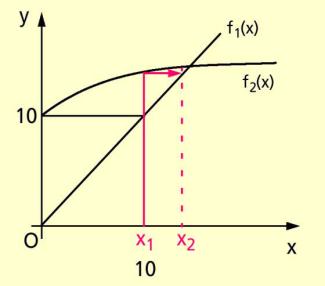
Es ist eine Umstellung gelungen, sodass die Gerade unter einem Winkel schneidet.
Eine Näherung sei . Es ist dann:
Im Bild 1 ist dargestellt, wie die Annäherung an die Schnittstelle erfolgt.
-
Annäherung an die Schnittstelle
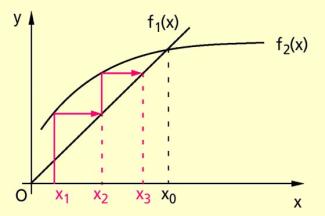
2. Fall:
Es ist eine Umstellung gelungen, sodass die Gerade unter einem Winkel schneidet.
Eine Näherung sei . Es ist dann:
Im Bild 2 ist dargestellt, wie die Annäherung an die Schnittstelle erfolgt.
Beispiel:
Gegeben ist die Gleichung .
Daraus folgt:
-
Grafische Veranschaulichung der Annäherung an die Schnittstelle