Quadratische Funktionen, Nullstellen

Wir betrachten zunächst quadratische Funktionen der Form $y = f (x) = a x^{2} + b x + c$ .
Man erhält $y = f (x) = x^{2} + b x + c$ bzw. durch Umbenennung
$y = f (x) = x^{2} + p x + q, p, q \in ℝ$ .
Um den Zusammenhang zwischen den reellen Zahlen p, q und den Nullstellen der jeweiligen quadratischen Funktionen bzw. den Schnittpunkten ihrer Graphen mit der x-Achse zu erkennen, ist es zweckmäßig, eine Fallunterscheidung durchzuführen.

Wir betrachten zunächst quadratische Funktionen $y = f (x) = a x^{2} + b x + c$ mit a = 1.
Man erhält
$y = f (x) = x^{2} + b x + c$ bzw. durch Umbenennung $y = f (x) = x^{2} + p x + q, p, q \in ℝ$ .
Um den Zusammenhang zwischen den reellen Zahlen p, q und den Nullstellen der jeweiligen quadratischen Funktionen bzw. den Schnittpunkten ihrer Graphen mit der x-Achse zu erkennen, ist es zweckmäßig, eine Fallunterscheidung durchzuführen.

Fall 1: p = 0, q = 0
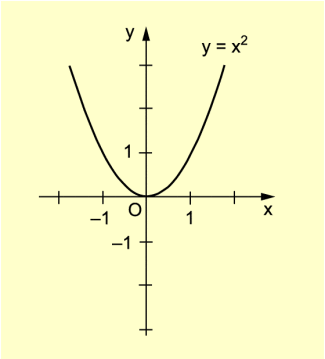
Man erhält die quadratische Funktion $y = f (x) = x^{2}$ (Bild 1).
Diese Funktion hat genau eine Nullstelle: x = 0

Nullstellen der quadratischen Funktion

Fall 2: p = 0; q $\neq$ 0
Es ergibt sich die Gleichung $y = f (x) = x^{2} + q, q \in ℝ$ , z. B. also
$y = f_{1} (x) = x^{2} + 1$ oder $y = f_{2} (x) = x^{2} - 4$ (Bild 2).
Man erkennt:
Ist q > 0, so existiert kein Schnittpunkt mit der x-Achse und demzufolge keine Nullstelle; für q < 0 dagegen gibt es zwei Abszissen-Schnittpunkte und folglich zwei Nullstellen.
Bei der rechnerischen Nullstellenbestimmung geht man in folgenden Schritten vor:

Allgemeiner Fall: $\begin{array}{l} f (x) = x^{2} + q \\ 0 = x^{2} + q x^{2} = - q \\ \|x\| = \sqrt{- q} und \\ {damit x}_{1} = + \sqrt{- q,} x_{2} = - \sqrt{- q} \end{array}$	Beispiel: $\begin{array}{l} g (x) = x^{2} - 4 \\ 0 = x^{2} - 4 x^{2} = 4 \\ \| x \| = 2 und \\ {damit x}_{1} = 2, x_{2} = - 2 \end{array}$
Die Funktion f hat also die Nullstellen $x_{1} = + \sqrt{- q} u n d x_{2} = - \sqrt{- q}$ . Ihr Graph schneidet die x-Achse in den Punkten $P_{1} (\sqrt{- q}; 0)$ und $P_{2} (- \sqrt{- q}; 0)$ .	Die Funktion g hat also die Nullstellen $x_{1} = 2$ und $x_{2} = - 2$ . Ihr Graph schneidet die x-Achse in den Punkten $P_{1} (2; 0)$ und $P_{2} (- 2; 0)$ .

Nullstellen der quadratischen Funktionen

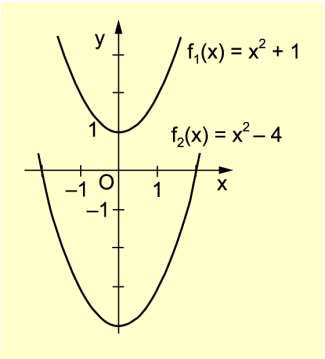
Fall 3: p $\neq$ 0, q = 0
Man erhält die Gleichung $y = f (x) = x^{2} + p x + q, p, q \in ℝ$ , z. B. also $y = g (x) = x^{2} + 2 x$ (Bild 3).
Um die Nullstellen der Funktionen zu ermitteln, ist die Gleichung

x^{2} + p x = 0

bzw.

x^{2} + 2 p x = 0

zu lösen. Man erhält:

x^{2} + p x = x (x + p) = 0

x^{2} + 2 p x = x (x + 2) = 0

Da ein Produkt genau dann gleich 0 ist, wenn mindestens ein Faktor den Wert 0 hat, folgt:

$\begin{array}{l} x_{1} = 0 {oder x}_{2} + p = 0, \\ {also x}_{2} = - p \end{array}$	$\begin{array}{l} x_{1} = 0 {oder x}_{2} + 2 = 0, \\ {also x}_{2} = - 2 \end{array}$
Die Funktion f hat demzufolge die Nullstellen $x_{1} = 0 und x_{2} = - p$ .	Die Funktion g hat also die Nullstellen $x_{1} = 0 und x_{2} = - 2$ .
Ihr Graph schneidet die x-Achse in den Punkten $P_{1} (0; 0)$ und $P_{2} (- p; 0)$ .	Ihr Graph schneidet die x-Achse in $P_{1} (0; 0)$ und $P_{2} (- 2; 0)$ .

Fall 4: p $\neq$ 0; q $\neq$ 0
Man erhält die Gleichung $y = f (x) = x^{2} + p x + q, p, q \in ℝ$ .
Die zugehörige Parabel hat den Scheitelpunkt $S (- \frac{p}{2}; - D)$
mit der Diskriminante $D = {(\frac{p}{2})}^{2} - q$ .
Kennt man D, dann kann man Aussagen über die Anzahl
der Nullstellen der zugehörigen quadratischen Funktion machen.
Es gilt:

Bild

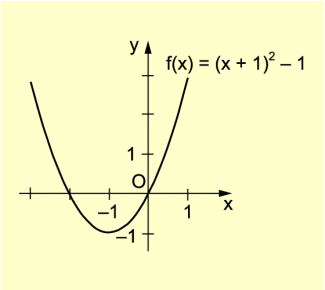
Für die quadratische Funktion $y = f (x) = x^{2} - 3 x - 1,75$ mit
p = –3 und q = –1,75 gilt:
D = 2,25 + 1,75 = 4 > 0
Das heißt: Die Funktion f besitzt zwei Nullstellen.

Nullstellen einer quadratischen Funktion

Nullstellenberechnung:

Bild

Stand: 2010
Dieser Text befindet sich in redaktioneller Bearbeitung.

Mathe Note verbessern?

Kostenlos bei Duden Learnattack registrieren und ALLES 48 Stunden testen.

Kein Vertrag. Keine Kosten.

40.000 Lern-Inhalte in Mathe, Deutsch und 7 weiteren Fächern
Hausaufgabenhilfe per WhatsApp
Original Klassenarbeiten mit Lösungen
Deine eigene Lern-Statistik
Kostenfreie Basismitgliedschaft

Mathe kostenlos lernen

Verwandte Artikel

Quadratische Funktionen, Nullstellen

Rechtliches

Einloggen