Das fermatsches Prinzip

Das von dem französischen Mathematiker und Juristen PIERRE DE FERMAT (1601-1665) gefundene Prinzip ist ein Extremalprinzip für die Ausbreitung von Licht. Es besagt:

Licht legt zwischen zwei Punkt immer den zeitlich kürzesten Weg zurück.

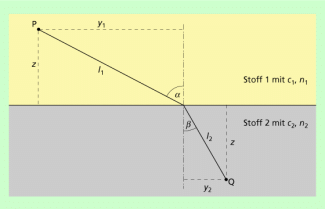
Dieser zeitlich kürzeste Weg ist nicht immer der geometrisch kürzeste Weg. Das hängt damit zusammen, dass die Zeit für einen Weg auch von der jeweiligen Lichtgeschwindigkeit beeinflusst wird. Diese Zusammenhänge sollen am Beispiel von Licht bei Brechung genauer dargestellt werden. Dazu wird der Weg des Lichtes zwischen zwei Punkten P und Q betrachtet (Bild 1).

Die optische Weglänge
Die geometrisch kürzeste Verbindung zwischen P und Q wäre eine Gerade. Befindet sich aber eine Grenzfläche zweier Stoffe zwischen P und Q, dann legt das Licht den in Bild 1 skizzierten Weg zurück. Man kann nun untersuchen, unter welchen Bedingungen das Licht in zwei verschiedenen Stoffen für einen Weg die gleiche Zeit benötigt. Die Laufzeit ergibt sich in einem optisch homogenen Stoff aus der geometrischen Weglänge l und der betreffenden Lichtgeschwindigkeit c:
$t_1=\frac{l_1}{c_1}{t}_2=\frac{l_2}{c_2}$
Geht man weiter davon aus, dass man für die Lichtgeschwindigkeiten
$\begin{array}{l}{c}_1=\frac{c_0}{n_1}\text{und}{c}_2=\frac{c_0}{n_2}\text{(}{c}_0\text{ist die Vakuumlichtgeschwindigkeit)}\\ \text{setzen kann}\text{, so erhält man:}\\ t_1=\frac{l_1\cdot n_1}{c_0}\text{bzw}\text{.}{t}_2=\frac{l_2\cdot n_2}{c_0}\\ \text{Gleiche Laufzeiten heißt dann:}\\ t_1=t_2\text{oder}{l}_1\cdot n_1=l_2\cdot n_2\end{array}$

Die Größe $n\cdot l$ wird als optische Weglänge oder auch als Lichtweg bezeichnet. Damit gilt allgemein:
Gleiche optische Weglängen werden in gleichen Zeiten zurückgelegt.

Optische Weglänge und Brechung
Betrachtet man die optische Weglänge zwischen den Punkten P und Q (Bild 1) so beträgt sie:
$\begin{array}{l}L=l_1\cdot n_1+l_2\cdot n_2\\ \text{Mit}{l}_1=\sqrt{{(y_1-y_0)}^2+z^2}\text{und}{l}_2=\sqrt{{(y_0-y_2)}^2+z^2}\\ \text{erhält man:}\\ L=n_1\sqrt{{(y_1-y_0)}^2+z^2}+n_2\sqrt{{(y_0-y_2)}^2+z^2}\end{array}$

Nun kann man diesen Lichtweg mit benachbarten Lichtwegen vergleichen, indem man die Lage des Punktes $y_0$ variiert. Mathematisch ergibt sich diese Variation als erste Ableitung $\frac{\text{d}L}{\text{d}{y}_0}.$
Die Ableitung ergibt:
$\begin{array}{l}\frac{\text{d}L}{\text{d}{y}_0}=-\frac{n_1(y_1-y_0)}{\sqrt{{(y_1-y_0)}^2+z^2}}+\frac{n_2(y_0-y_2)}{\sqrt{{(y_0-y_2)}^2+z^2}}\\ \text{Mit}\frac{y_1-y_0}{l_1}=\sin \alpha \text{und}\frac{y_0-y_2}{l_2}=\sin \beta \text{erhält man:}\\ \frac{\text{d}L}{\text{d}{y}_0}=-n_1\cdot \sin \alpha +n_2\cdot \sin \beta \\ \text{Wegen der Gültigkeit des Brechungsgesetzes wird}\\ \frac{\text{d}L}{\text{d}{y}_0}=0\end{array}$
Das bedeutet: Bei der Brechung von Licht an einer Grenzfläche ist die optische Weglänge im Vergleich mit möglichen benachbarten Wege ein Extremwert, genauer: ein Minimum.
Die Aussage darüber, dass die optische Weglänge zwischen zwei Punkten ein Minimum ist, gilt allgemein und wird dann als fermatsches Prinzip bezeichnet. Es lässt sich folgendermaßen formulieren:

Die optische Weglänge zwischen zwei Punkten ist ein Minimum.

Gleichwertig ist die oben bereits genannte Formulierung:

Licht legt zwischen zwei Punkt immer den zeitlich kürzesten Weg zurück.