Digitale Grundschaltungen
Elektronische Schaltungen sind Zusammenfügungen von aktiven und passiven Bauelementen zu einem Gebilde, welches eine angestrebte Funktion realisieren kann. Man kann sie nach ihrer Herstellungstechnologie und nach den in ihnen verarbeiteten Signalen unterscheiden.
Werden sie aus einzelnen Bauelementen zusammengesetzt, sodass diese auch grundsätzlich wieder aus der Schaltung herausgelöst werden könnten, spricht man von diskreten Schaltungen. Werden sie dagegen so realisiert, dass das einzelne Bauelement grundsätzlich nicht herausgelöst werden kann, die Gesamtschaltung sich also wie ein einziges Bauelement verhält, nennt man sie integrierte Schaltungen.
Unterschieden wird dabei nach der Art der verarbeiteten Signale zwischen analogen und digitalen Schaltungen. Letztere werden in kombinatorische und sequenzielle Schaltungen unterteilt.
Digitale Signale
Nach DIN 19226 repräsentieren Signale Informationen. Durch ein Signal wird der Werteverlauf einer physikalischen Größe abgebildet. Elektrische Signale sind als Abbildungen des Werteverlaufs physikalischer Größen durch Ströme bzw. Spannungen. Erfolgt die Abbildung auf eine stetige Funktion, spricht man von analogen, andernfalls von diskreten Signalen.
-
Eine ODER-Schaltung ist ein Beispiel für eine digitale Schaltung zur Realisierung logischer Verknüpfungen
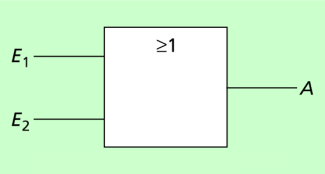
Diskrete Signale (wir nehmen solche mit 8 verschiedenen Werten an) werden an den Eingang eines sogenannten Codierers gegeben, der am Ausgang nur zweiwertige (binäre) Signale liefert. Für 8 Eingangswerte sind 3 Ausgangsleitungen erforderlich
(). Diese 3 Leitungswerte bilden ein binäres Wort. Jedes binäre Wort mit einer konkreten inhaltlichen Bedeutung heißt digitales Signal. Wenn die angenommenen 8 diskreten Werte für in Volt gemessene Spannungen stehen, bedeutet LHH = 3 V. Dabei sind L und H die Zeichen, die für die beiden verschiedenen Werte eines binären Signals stehen.
Werden diese Werte durch Spannungen repräsentiert, so steht L und auch H immer für ein ganzes Spannungsintervall. Man spricht vom L-Pegel bzw. vom H-Pegel.
H-Pegel ist derjenige der beiden Spannungsbereiche, der näher an liegt.
Beide Pegel sind entweder positiv (p-Logik) oder negativ (n-Logik).
Welche Werte sie im Einzelnen umfassen, hängt von den für die Schaltungen verwendeten Halbleitermaterialien und ihrer Herstellungstechnologie ab. Eine weitverbreitete Schaltkreisgruppe (Familie) ist die TTL-Familie (Transistor-Transistor-Logik), eine mit positiven Pegeln arbeitende Reihe. In ihr setzt man auch L = 0 und H = 1.
Verknüpfungen zwischen den Variablen 0 und 1 werden durch eine zweiwertige Logik, die sogenannte boolesche Algebra , beschrieben.
Für das Verständnis der Arbeitsweise digitaler Grundschaltungen sind einige Kenntnisse der Verknüpfung binärer Größen unerlässlich. Deshalb sind nachfolgend einige Grundlagen der boolschen Algebra dargestellt.
Grundbegriffe der booleschen Algebra
Darin werden Verknüpfungen zwischen den Elementen 0 und 1 der Menge erklärt.
Negation: , bezeichnet als „a negiert“ bzw. „nicht a“
Konjunktion: , bezeichnet als „a und b“
Disjunktion: , bezeichnet als „a oder b“
Oberhalb der Trennlinie stehen Axiome, darunter daraus ableitbare Gesetze.Deren Bestätigung ist durch unmittelbares Einsetzen möglich, denn es gibt immer nur endlich viele Belegungen.
Dass damit nicht die Gesamtheit der Beziehungen in der booleschen Algebra dargestellt ist, versteht sich von selbst. Es sind lediglich solche ausgewählt, die für das Verständnis der folgenden Betrachtungen unbedingt erforderlich sind.
Kombinatorische Schaltungen
Kombinatorische Schaltungen verfügen über (mindestens) zwei Eingangs- und eine Ausgangsleitung. Das ist in Form einer Black Box in Bild 2 skizziert. Die erforderlichen Spannungsanschlüsse werden in der Regel nicht gezeichnet.
-
Black-Box - Darstellung einer kombinatorischen Schaltung
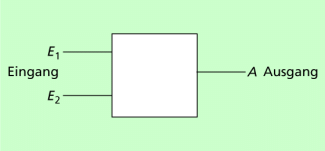
Die Eingangsleitungen können unabhängig voneinander mit 0 oder 1 belegt werden. Auf der Ausgangsleitung A treten ebenfalls nur 0 und 1 auf. Für derartige Systeme gibt es also nur 16 verschiedene Ein- und Ausgangsbelegungen. Darunter sind jedoch mehrere triviale sowie Wiederholungen lediglich mit vertauschten Eingangsleitungen. Dadurch bleiben nur 9 echte Verknüpfungen übrig. Diese sind als Übersicht in Bild 3 zusammenfassend dargestellt.
-
Überblick über echte kombinatorische Schaltungen mit zwei Eingängen
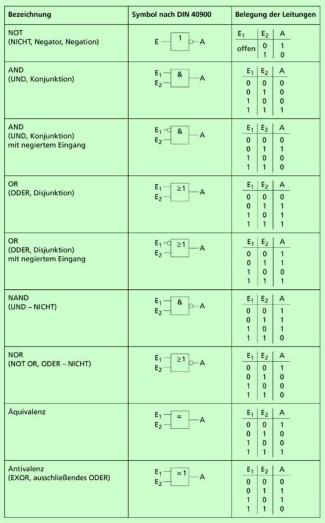
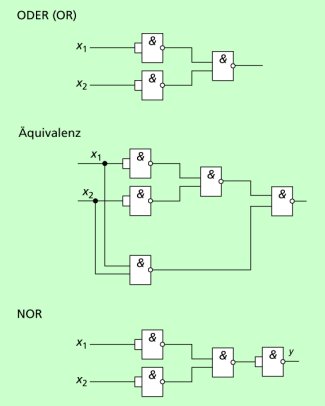
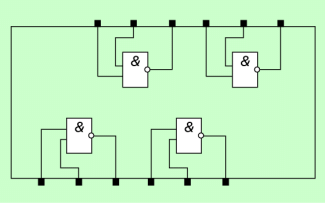
Es lässt sich nachweisen, dass sich alle neun Schaltungen allein mit NAND bzw. mit NOR realisieren lassen. In Bild 4 ist das beispielhaft für einige Schaltungen mit Nutzung von NAND darstellt.
Der entscheidende Aspekt, der aus dieser Tatsache folgt, ist der, das es möglich ist, beliebige kombinatorische Schaltungen auf einer Chipfläche dadurch zu erzeugen, dass man in einem ersten technologischen Prozess nur NAND auf dem Chip erzeugt, die in einer zweiten Schrittfolge in der richtigen Weise untereinander verbunden werden. So gelingt es, auf einer Chipfläche einerseits eine große Menge gleicher kombinatorischer Schaltungen zu erzeugen, die dann nach dem Trennen zu jeweils einem Baustein verarbeitet werden können.
Andererseits ist es aber auch möglich, auf einer Chipfläche eine große Menge verschiedener kombinatorischer Schaltungen zu realisieren, die in einem abschließenden Schritt zu einem neuen komplexen Gebilde zusammengefasst werden können.
Etwas vereinfacht lässt sich also sagen, dass digitale Schaltungen in integrierter Technik durch vielfache Wiederholungen der NAND-Struktur auf einem Chip realisiert werden können. Entsprechend wäre das prinzipiell auch mit NOR-Strukturen möglich.
Der entscheidende Gewinn dieser integrierten Schaltungstechnik ist der Umstand, dass sich das fertige Objekt hinsichtlich seiner mittleren Lebensdauer wie ein einzelnes Bauelement verhält. Wollte man derartige komplexe Schaltungen aus der erforderlichen großen Anzahl von einzelnen Transistoren, Widerständen und Verbindungsleitungen in diskreter Schaltungstechnologie erzeugen, sinkt mit der wachsenden Anzahl von Einzelelementen und Verbindungen die mittlere Lebensdauer (also die Zeit einer vollen Funktionsfähigkeit) rapide. Außerdem würde ein derartiger Aufbau zu einem großen Volumen führen.
Neben weiteren Vorzügen haben die beiden Komponenten - die Realisierung sehr komplexer digitaler Schaltungen aus wenigen Grundstrukturen und die integrierte Herstellungstechnologie - der Digitaltechnik zu ihrer heutigen Bedeutung verholfen.
Zwei alltägliche Probleme, nämlich eine elementare Waschmaschinensteuerung und das automatische Auslösen einer Sprinkleranlage, sollen mithilfe digitaler Schaltungen gelöst werden.
Waschmaschinensteuerung
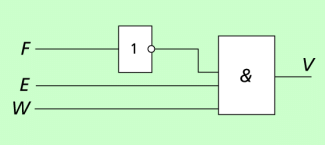
Die Darstellung zur Waschmaschinensteuerung ist vereinfacht. Es erfolgt eine Beschränkung auf eine der vielen Funktionen.
Wir betrachten zunächst den Startvorgang „Einfüllen des Wassers“. Dabei sind offensichtlich folgende Sachverhalte zu berücksichtigen:
- Es muss ein bestimmtes Waschprogramm „W“ ausgewählt werden.
- Es muss die Wäscheeinfüllöffnung verschlossen sein.
- Es muss das Ventil „V“ der Wasserleitung geöffnet werden.
- Bei Erreichen eines bestimmten Füllstandes „F“ muss das Ventil wieder schließen.
- Die zu beeinflussende Größe ist die Ventilstellung des Wasserzulaufs. Sie darf die beiden Werte „zu“ bzw. „auf“ annehmen.
Die beeinflussenden Größen sind:
- der Programmwahlschalter W,
- der Kontakt der Wäscheeinfüllöffnung E,
- der Wasserfüllstand F.
Diese drei Größen werden binäre Werte zugeordnet:
W = 0, kein Programm ausgewählt
W = 1, ein Waschprogramm gewählt.
E = 0, Einfüllöffnung unverschlossen
E = 1, Einfüllöffnung geschlossen
F = 0, Endfüllstand noch nicht erreicht
F = 1, Endfüllstand erreicht
Die davon beeinflusste Größe ist die Ventilstellung V:
V = 0, Ventil zu
V = 1, Ventil geöffnet.
Das ergibt eine formale Belegungstabelle mit Zeilen.
| Zeile | W | E | F | V |
| 1 | 0 | 0 | 0 | 0 |
| 2 | 0 | 0 | 1 | 0 |
| 3 | 0 | 1 | 0 | 0 |
| 4 | 1 | 0 | 0 | 0 |
| 5 | 1 | 1 | 0 | 1 |
| 6 | 1 | 0 | 1 | 0 |
| 7 | 0 | 1 | 1 | 0 |
| 8 | 1 | 1 | 1 | 0 |
Praktisch dürfen die Zeilen 5 und 8 nur allein durch die Steuerung realisiert werden. Zeile 5 öffnet das Ventil, Zeile 8 schließt es. Die Zeile 5 lässt sich durch eine UND-Verknüpfung ausdrücken: . Wie man durch Einsetzen unmittelbar nachprüfen kann, öffnet allein die Belegung aus Zeile 5 das Ventil, mit der Belegung aus Zeile 8 wird es geschlossen.
-
Darstellung einiger kombinatorischer Schaltungen mit NAND
Eine Realisierung zeigt Bild 5. Natürlich werden in einer vollständigen Steuerung der Waschmaschinenfunktionen durch den Wahlschalter W nicht nur die Wasserzufuhr, sondern auch die Wassertemperatur (Heizung an/aus), die Wäschebewegung (Motor an/aus) usw. beeinflusst. Das sind strukturell aber ähnliche Schritte wie die bereits beschriebenen.
Steuerung einer Sprinkleranlage
In einer Lagerhalle werde eine Sprinkleranlage über zwei Rauchsensoren gesteuert. Wenn mindestens einer der beiden Sensoren anspricht, möge das Ventil der Löscheinrichtung geöffnet werden. Bezeichnet man die Sensoren mit S und T, das Ventil mit V und verabredet, dass das Fehlen von Rauch in S und T den Wert 0, sonst 1 liefert, die geschlossene Stellung von V wieder 0, die geöffnete 1 liefern soll. Das ergibt eine 4-zeilige Belegungstabelle:
| Zeile | S | T | V |
| 1 | 0 | 0 | 0 |
| 2 | 0 | 1 | 1 |
| 3 | 1 | 0 | 1 |
| 4 | 1 | 1 | 1 |
Wie man aus der Tabelle unmittelbar ablesen kann, gilt Die gleiche Verknüpfung bestünde auch dann, wenn eine größere Anzahl von Sensoren zum Einsatz kommen würde. Es wäre aber auch möglich gewesen, für V die Beziehung abzulesen. Denn unabhängig von der Belegung hat einer der drei Terme immer den Wert 1. Da sie durch ODER verknüpft sind,wäre also V = 0 nur für S = T = 0, sonst immer 1. Der Schaltungsaufwand wäre aber weitaus höher.
Man stößt also hier auf das Problem, dass es offenbar zu einer Aufgabenstellung durchaus verschiedene richtige Lösungen geben kann, von denen eine den geringsten Schaltungsaufwand erfordert. Derartige Schaltungsoptimierungen sind mittels der booleschen Algebra möglich.
Die digitale Grundstruktur NAND
Diese Struktur gibt es sowohl in unipolarer als auch in bipolarer Ausführung und darin jeweils in verschiedenen Schaltkreisfamilien - also Systemen mit bestimmten übereinstimmenden Parametern, wie etwa Leistung und Schaltzeit.
-
Darstellung einer Waschmaschinensteuerung
Betrachtet wird stellvertretend für alle das NAND der TTL-Standard-Reihe.
Der einfachste Schaltkreis darin ist der SN 7400, der in einem 14-poligen DIL-Gehäuse 4 NAND mit je zwei Eingängen und je einem Ausgang sowie die Spannungsanschlüsse enthält. Im Bild 6 ist er dargestellt.
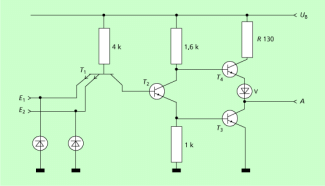
Seine Innenschaltung realisiert mithilfe eines Mehremittertransistors ein UND mit nachgeschaltetem Negator (das ist eine vereinfachte Beschreibung). Ihr konkreter Aufbau ist in Bild 7 dargestellt.
-
Pin-Belegung der IS SN 7400
Alle IC der Standard-TTL haben eine Betriebsspannung von + 5 V und sind miteinander kompatibel. Für alle digitalen Schaltkreise ist realisiert, dass der höchste Ausgangsspannungswert für L-Pegel sicher vom Eingang eines IC der gleichen Familie als L-Pegel erkannt wird. Entsprechendes gilt für die H-Pegel.
Die absoluten Werte für die einzelnen Schaltkreisfamilien sind den zugehörigen Datenblättern zu entnehmen. Insbesondere ist für den Ausgangs-H-Pegel zu beachten, dass er mit der Strombelastung des Ausgangs sinkt. Deshalb sind die Belastungsgrenzen, die der Hersteller vorgibt, sorgfältig zu beachten.
Neben der Möglichkeit, binäre Signalwerte kombinatorisch zu verknüpfen, sind spezielle Schaltungen mit NAND auch in der Lage, einen analogen Eingangssignalverlauf in ein binäres Ausgangssignal zu verwandeln.
Eine weitere Anwendungsmöglichkeit für NAND besteht in der Möglichkeit, sie mithilfe einer kleinen Außenbeschaltung zur ständigen Erzeugung von Rechteckimpulsen (Taktgeneratoren) zu veranlassen.
-
Innenschaltung eines NAND in Bipolartechnik
Suche nach passenden Schlagwörtern
- IC
- Codierer
- Äquivalenz
- integrierter Schaltkreis
- boolsche Algebra
- Negator
- Sprinkleranlage
- L-Pegel
- TTL-Familie
- Mehremittertransistor
- passive Bauelemente
- aktive Bauelemente
- NAND
- NICHT
- OR
- Digitaltechnik
- H-Pegel
- AND
- Konjunktion
- NOR
- Signale
- Digitale Grundschaltungen
- n-Logik
- Antivalenz
- NAND der TTL-Standard-Reihe
- digitales Signal
- EXOR
- Disjunktion
- Negation
- Chip
- Lebensdauer
- kombinatorische Schaltungen
- Waschmaschinensteuerung
- Taktgeneratoren
- Not
- p-Logik
- Rechteckimpulse

