Innere Energie
Die innere Energie gibt an, wie groß die in einem abgeschlossenen System (Körper) gespeicherte Energie ist.
Formelzeichen: U
Einheit: ein Joule (1 J)
Sie ist die Gesamtenergie aller Teilchen (Atome, Moleküle) eines Körpers und setzt sich damit aus der Summe der Bewegungsenergien bei Translation, Rotation und Schwingungen, der potenziellen Energien und der Bindungsenergien zusammen.
Bei Gasen wird die innere Energie im Wesentlichen von den Bewegungsenergien der Teilchen bestimmt.
Die Größe innere Energie
Ein thermodynamisches System bzw. ein Körper kann in unterschiedlicher Weise charakterisiert werden. Eine Möglichkeit besteht darin, seine Temperatur anzugeben. Die Temperatur besagt aber noch nichts über die Energie, die in einem System bzw. in einem Körper gespeichert ist. Diese wird mit einer Größe erfasst, die RUDOLF CLAUSIUS (1822-1888) um 1850 in die Physik eingeführt hat und die man als innere Energie bezeichnet.
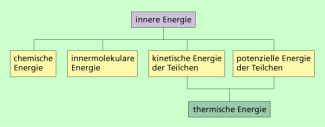
Innere Energie ist damit die Gesamtenergie, die in einem System oder Körper vorhanden ist. Sie setzt sich demzufolge aus verschiedenen Bestandteilen zusammen. Sie ist die Summe aus:
- kinetische Energien der Teilchen (Atome, Moleküle) des Systems (Energie der Translation, Energie der Rotation, Schwingungsenergie),
- potenzielle Energien der Teilchen,
- Bindungsenergien der Teilchen, die man manchmal noch in innermolekulare Energie und chemische Energie unterteilt.
Manchmal wird auch der Terminus thermische Energie genutzt. Damit ist in der Regel der Teil der inneren Energie gemeint, der unmittelbar mit der Temperatur verknüpft ist (Bild 1).
Innere Energie von Gasen
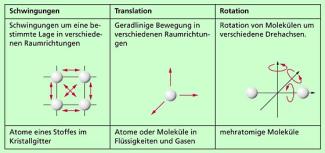
Bei Gasen wird die innere Energie im Wesentlichen von den Bewegungsenergien der Teilchen bestimmt. In Bild 2 sind die verschiedenen Möglichkeiten dargestellt. Da die Temperatur ein Maß für die mittlere kinetische Energie der Teilchen eines Gases ist, kann sie auch als Maß für die innere Energie eines Gases angesehen werden. Dabei entfällt auf jeden Freiheitsgrad der Bewegung der gleiche Anteil an mittlerer kinetischer Energie (Gleichverteilungssatz). Unter einem Freiheitsgrad versteht man eine der möglichen Bewegungen, die ein Atom oder ein Molekül ausführen kann. So haben die Teilchen des idealen Gases (einatomiges Gas) drei Freiheitsgrade der Translation; sie können sich in drei unterschiedliche Raumrichtungen bewegen (Bild 2 Mitte). Bei zweiatomigen Gasen (Hantelmodell) kommen drei Freiheitsgrade der Rotation hinzu (Bild 2 rechts), wobei die Rotation um die Längsachse vernachlässigt werden kann und damit nur zwei Freiheitsgrade berücksichtigt werden.
Für jeden Freiheitsgrad der Bewegung gilt:
Sind N Teilchen vorhanden, so erhält man die Gesamtenergie (innere Energie) durch Multiplikation der Energie eines Teilchens mit der Teilchenanzahl N. Damit ergibt sich:
- Beim idealen Gas und damit auch bei einatomigen Gasen sind drei Freiheitsgrade der Translation vorhanden. Demzufolge beträgt die innere Energie:
- Ein zweiatomiges Gas (Hantelmodell) hat drei Freiheitsgrade der Translation und zwei der Rotation. Demzufolge gilt für dessen innere Energie:
- Drei- und mehratomige Gase haben je drei Freiheitsgrade der Translation und der Rotation und damit die innere Energie:
Bei hohen Temperaturen werden die Atome in den Molekülverbindungen der mehratomigen Gase auch zu Schwingungen angeregt. Dann müssen diese Freiheitsgrade bei der Berechnung der inneren Energie ebenfalls berücksichtigt werden.
Innere Energie von Flüssigkeiten und Festkörpern
In Flüssigkeiten und Festkörpern ist der Abstand der Teilchen viel geringer als bei Gasen und die Bewegung der Teilchen eingeschränkt. Daher müssen auch die Bindungsenergien und die potenziellen Energien der Teilchen als Formen der inneren Energie berücksichtigt werden.
Bei der Änderung des Aggregatszustandes eines Stoffes muss z.B. Wärme in Form von Schmelz- oder Verdampfungswärme zugeführt werden, ohne dass sich die Temperatur ändert. Diese Wärme erhöht die innere Energie, indem sie Bindungs- und Oberflächenenergien der Teilchen kompensiert. Damit ist auch klar, dass zwei Körper eines Stoffes mit gleicher Temperatur unterschiedliche innere Energien haben können. So haben beispielsweise die gleichen Massen Wasser und Eis bei 0 °C verschiedene innere Energien: Die von Wasser ist größer als die von Eis.
Durch die Einführung der Größe innere Energie U eines Körpers gelang es, zwei grundsätzliche Probleme zu klären:
- Zum einen konnte der Zusammenhang zwischen Wärme und mechanischer Energie in einem abgeschlossenen System angegeben werden (1. Hauptsatz der Thermodynamik).
- Zum anderen wird erklärt, dass die Umwandlung von Wärme in mechanischer Energie durch die Änderung der inneren Energie des Systems erfolgen kann.
Die Aufspaltung der Energie eines Körpers in einen makroskopischen Anteil (z.B. der Bewegungsenergie des Körpers) und einen mikroskopischen Anteil (der innere Energie) führte schließlich zu der Formulierung des allgemeinen Prinzips von der Erhaltung der Energie (Energieerhaltungssatz) durch HERMANN VON HELMHOLTZ. Er kam zufolgender Formulierung:
In einem abgeschlossenen System kann Energie nicht erzeugt und nicht vernichtet, sondern nur von einer Form in andere Formen umgewandelt werden. Die Gesamtenergie des Systems bleibt konstant.
Suche nach passenden Schlagwörtern
- Berechnung
- Energieerhaltungssatz
- Gleichverteilungssatz
- potenzielle Energie
- Helmholtz
- innere Energie
- zweiatomiges Gas
- thermische Energie
- Festkörper
- Rotationsenergie
- einatomiges Gas
- kinetische Energie
- potentielle (neue Rechtschreibung: potenzielle) Energie
- Bindungsenergie
- Schwingungsenergie
- Flüssigkeit
- Freiheitsgrad
- fester Körper
- RUDOLF CLAUSIUS
- ideales Gas
- Rechenbeispiel
- Gesamtenergie