Lorentz-Kraft
Auf alle geladenen Teilchen oder Körper, die sich in einem magnetischen Feld nicht parallel zu den magnetischen Feldlinien bewegen, wirkt eine Kraft. Diese Kraft bezeichnet man nach dem niederländischen Physiker HENDRIK LORENTZ (1853-1928), der sie gegen Ende des 19. Jahrhunderts näher untersucht hat, als LORENTZ-Kraft. Für die LORENTZ-Kraft gilt allgemein:
Betrachtet man nur den Betrag der Kraft, dann kann man auch schreiben:
Beträgt der Winkel zwischen derGeschwindigkeit v und der magnetischer Flussdichte B (Richtung der Feldlinien) gerade 90°, dann erhält man:
Bewegen sich Elektronen oder Protonen im magnetischen Feld so kann man für die Ladung Q die Elementarladung e einsetzen.
Material zum Thema
Aus den genannten Gleichungen folgt:
- Bewegen sich geladene Körper oder Teilchen parallel zu den Feldlinien des magnetischen Feldes, stimmt also die Richtung der Geschwindigkeit mit der der magnetischen Flussdichte überein, so ist die LORENTZ-Kraft null. Geladene Körper oder Teilchen werden durch das Magnetfeld nicht beeinflusst.
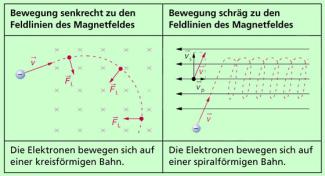
- Bei senkrechtem Eintritt in das Feld - der Winkel zwischen Geschwindigkeit und Feldrichtung beträgt dann 90° - wirkt in einem homogenen Feld eine konstante LORENTZ-Kraft stets senkrecht zur Bewegungsrichtung. Sie wirkt damit als Radialkraft. Die geladenen Körper oder Teilchen bewegen sich auf einer Kreisbahn (Bild 2 links).
- Bei schrägem Eintritt in das Magnetfeld (Bild 2 rechts) wirkt, ein homogenes Magnetfeld vorausgesetzt, eine konstante LORENTZ-Kraft. Dabei kann man die Geschwindigkeit in zwei Komponenten zerlegen: Die Geschwindigkeitskomponente senkrecht zu den Feldlinien bewirkt eine konstante Kraft senkrecht zur Bewegungsrichtung und führt damit zu einer kreisförmigen Bewegung. Die Geschwindigkeitskomponente parallel zu den Feldlinien bewirkt, dass die Kreisbahn „auseinandergezogen“ wird (Bild 2 rechts). Damit entsteht eine spiralförmige Bahn.
Linke-Hand-Regel oder Rechte-Hand-Regel?
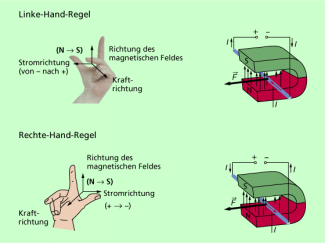
Bewegen sich geladene Körper oder Teilchen senkrecht zur Richtung des Magnetfeldes, so kann man die Richtung der LORENTZ-Kraft mithilfe der Linke-Hand-Regel oder auch der Rechte-Hand-Regel ermitteln (Bild 3).
Welche Variante man wählt, ist eine Frage der Vereinbarung. Der Unterschied zwischen den beiden besteht darin, dass man bei der Linke-Hand-Regel von der Bewegungsrichtung negativ geladener Teilchen (Elektronen) ausgeht, bei der Rechte-Hand-Regel aber von der Bewegungsrichtung positiv geladener Teilchen. Will man also beispielsweise mit der Rechte-Hand-Regel die Richtung der Kraft auf Elektronen bestimmen, so muss man den Daumen entgegen ihrer Bewegungsrichtung halten.
Hat man sich z.B. auf die Linke-Hand-Regel festgelegt, dann gilt:
- Der Daumen der linken Hand zeigt in der Bewegungsrichtung negativ geladener Teilchen (von Minus nach Plus)
- Der Zeigefinger der linken Hand zeigt in Richtung des magnetischen Feldes, das stets vom Nord- zum Südpol orientiert ist.
- Der Mittelfinger der linken Hand weist in Richtung der LORENTZ-Kraft.
Die genannte Regel wird mitunter auch als UVW-Regel bezeichnet. Die drei Buchstaben stehen für Ursache, Vermittlung und Wirkung und sind folgendermaßen zu interpretieren:
- Ursache ist die Bewegung der geladenen Körper bzw. Teilchen (Daumen).
- Vermittlung ist das Magnetfeld, das vorhanden sein muss, wenn auf Kraftwirkung auftreten soll (Zeigefinger).
- Die Wirkung ist die Lorentz-Kraft, deren Richtung durch den Mittelfinger angegeben wird.
Kraft auf stromdurchflossene Leiter
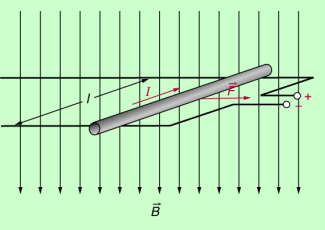
Ein Stromfluss in einem elektrischen Leiter ist gleichbedeutend mit der Bewegung von Ladungsträgern. Befindet sich dieser Leiter in einem äußeren Magnetfeld, dann muss demzufolge eine LORENTZ-Kraft auf ihn wirken (Bild 4). Anders als bei der Kraft, die auf einen einzelnen Ladungsträger wirkt, befinden sich im stromdurchflossenen Leiter stets sehr viele Elektronen gleichzeitig im magnetischen Feld. Die LORENTZ-Kraft ist deshalb die Summe aller Teilkräfte auf die einzelnen Elektronen. Befindet sich der Leiter senkrecht zu den magnetischen Feldlinien und bezeichnet N die Anzahl aller geladenen Teilchen, die sich gleichzeitig innerhalb des Feldes aufhalten, gilt für den Betrag der LORENTZ-Kraft:
Diese Gleichung lässt sich folgendermaßen umformen, wobei wir von einem Strom konstanter Stärke durch den Leiter ausgehen:
Bedeutung der LORENTZ-Kraft
Mithilfe der LORENTZ-Kraft kann man z.B. die Wirkungsweise von Gleichstrommotoren erklären. Bei Elektronenstrahlröhren kann man ermitteln, in welche Richtung der Elektronenstrahl abgelenkt wird, wenn er ein Magnetfeld durchläuft.
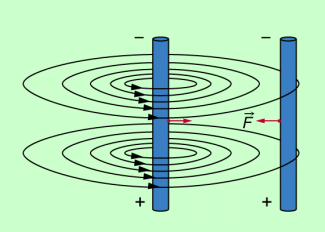
LORENTZ-Kraft und Linke-Hand-Regel können auch genutzt werden, um die Richtung der Kraft zwischen zwei stromdurchflossenen Leitern zu bestimmen (Bild 5). Um einen stromdurchflossenen Leiter existiert ein Magnetfeld. Bringt man nun in dieses Magnetfeld einen weiteren stromdurchflossenen Leiter, so wirkt auf diesen eine Kraft, die man nach der Linke-Hand-Regel bestimmen kann. Stromdurchflossene Leiter ziehen sich bei gleicher Stromrichtung an und stoßen sich bei entgegengesetzter Stromrichtung ab.
Die Kräfte zwischen stromdurchflossenen Leitern werden zur Definition der Einheit Ampere genutzt, die eine der sieben Grundeinheiten des Internationalen Einheitensystems ist. Die Definition der Grundeinheit Ampere lautet:
Das Ampere ist die Stärke eines konstanten elektrischen Stromes, der, durch zwei parallele, geradlinige, unendlich lange und im Vakuum im Abstand von einem Meter voneinander angeordnete Leiter von vernachlässigbar kleinem, kreisförmigen Querschnitt fließend, zwischen diesen Leitern je einem Meter Leiterlänge eine Kraft von hervorrufen würde.
Ein Angebot von 