Millikan-Versuch zur Bestimmung der Elementarladung

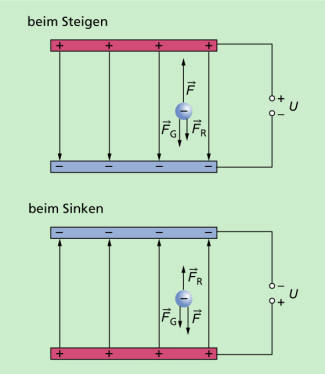
Der Versuch von MILLIKAN

Mit einem völlig anderen Verfahren gelang es dem amerikanischen Physiker ROBERT ANDREWS MILLIKAN (1868-1953), in den Jahren 1909 bis 1913 erstmals die Elementarladung e relativ genau zu bestimmen. Er nutzte dazu die Tröpfchenmethode, der Versuch wird heute als MILLIKAN-Versuch bezeichnet. MILLIKAN erhielt für die Präzisionsmessung der Elementarladung 1923 den Nobelpreis für Physik. Das Prinzip des MILLIKAN-Versuches ist in Bild 1 dargestellt. In ein senkrecht gerichtetes elektrisches Feld werden Öltröpfchen gesprüht, die sich durch Reibung aufladen. Sie werden durch ein Mikroskop mit einer senkrecht angebrachten Skala beobachtet. Liegt kein elektrisches Feld an, sinken die Tröpfchen unterschiedlich schnell nach unten. Nach Anlegen eines Feldes sinken einige Tröpfchen schneller, andere schweben oder steigen. Nach Umpolen der Spannung kehrt sich die Bewegungsrichtung um.

Die quantitativen Zusammenhänge
Bei schwebenden Tröpfchen sind Gewichtskraft und Feldkraft gleich groß. Es gilt also:

$\begin{array}{l}\text{Gewichtskraft}{F}_G=\text{Feldkraft}F\\ m\cdot g=Q\cdot E\\ \text{Beträgt die Ladung eines Öltröpfchens}Q=N\cdot e\text{und die}\\ \text{elektrische Feldstärke in einem Plattenkondensator}E=\frac{U}{d},\\ \text{so erhält man:}\\ m\cdot g=N\cdot e\cdot \frac{U}{d}\text{und nach der Elementarladung}e\text{umgestellt:}\\ e=\frac{m\cdot g\cdot d}{N\cdot U}\end{array}$

Damit könnte man die Elementarladung e bestimmen. Das Problem besteht allerdings in der Ermittlung der Masse. Um es zu lösen, wandte MILLIKAN folgenden „Trick“ an: Neben der Gewichtskraft und der Feldkraft wirkt auf die kleinen Tröpfchen auch die Luftreibungskraft. Sie bewegen sich gleichförmig nach oben (Bild 1 oben), wenn diese Reibungskraft
$F_{\text{R}}=F-F_{\text{G}}\text{(1)}$
und gleichförmig nach unten (Bild 1 unten), wenn:
$F_{\text{R}}=F+F_{\text{G}}\text{(2)}$
Nach dem stokeschen Gesetz kann man für die Reibungskraft schreiben:
$\begin{array}{l}{F}_{\text{R}}=6\pi \cdot \eta \cdot r\cdot v\\ \text{Dabei ist}\eta \text{die dynamische Viskosität ("Zähigkeit des Stoffes")}\text{,}\\ r\text{der Tröpfchenradius und}v\text{die Geschwindigkeit der Tröpfchen}\text{.}\end{array}$

Aus den Kräftegleichgewichten (1) und (2) kann man unter Einbeziehung der zuletzt genannten Gleichung für die Reibungskraft die Geschwindigkeit beim Sinken und Steigen ermitteln:

$\begin{array}{l}\text{beim Steigen:}\text{beim Sinken:}\\ 6\pi \cdot \eta \cdot r\cdot v=N\cdot e\cdot E-m\cdot g6\pi \cdot \eta \cdot r\cdot v=N\cdot e\cdot E+m\cdot g\\ v_1=\frac{N\cdot e\cdot E-m\cdot g}{6\pi \cdot \eta \cdot r}{v}_2=\frac{N\cdot e\cdot E+m\cdot g}{6\pi \cdot \eta \cdot r}\\ \text{Um}N\cdot e=Q\text{zu bestimmen}\text{, bildet man}{v}_{\text{1}}+v_2\text{und}{v}_{\text{1}}-v_2.\\ \text{Aus den Gleichungen wird das schwer messbare}r\text{eliminiert und}\\ \text{die Gleichung nach}Q\text{aufgelöst}\text{.}\end{array}$
Die Herleitung ist etwas aufwändig. Deshalb sind hier nur die wichtigsten Schritte genannt.
Bildet man die Summe bzw. die Differenz der beiden Geschwindigkeiten, so erhält man:
$\begin{array}{l}{v}_1+v_2=\frac{Q\cdot E}{3\pi \cdot \eta \cdot r}\text{(1)}{v}_2-v_1=\frac{m\cdot g}{3\pi \cdot \eta \cdot r}\text{(2)}\\ \text{Aus (1) ergibt sich durch Umstellung nach}r:\\ r=\frac{Q\cdot E}{3\pi \cdot \eta (v_1+v_2)}\\ \text{Eingesetzt in (2) erhält man:}\\ v_2-v_1=\frac{m\cdot g\cdot 3\pi \cdot \eta (v_1+v_2)}{3\pi \cdot \eta \cdot Q\cdot E}\text{oder vereinfacht:}\\ v_2-v_1=\frac{m\cdot g\cdot (v_1+v_2)}{Q\cdot E}\\ \text{Die Umstellung nach}Q\text{ergibt:}\\ Q=\frac{m\cdot g\cdot (v_1+v_2)}{E(v_2-v_1)}\end{array}$

$\begin{array}{l}\text{Mit}E=\frac{U}{d}\text{und}m=\frac{4}{3}\pi \cdot r^3\cdot \rho \text{erhält man:}\\ Q=\frac{4\pi \cdot r^3\cdot \rho \cdot g(v_1+v_2)d}{3U(v_2-v_1)}\\ \text{Mit}r=\frac{Q\cdot E}{3\pi \cdot \eta (v_1+v_2)}\text{ergibt sich schließlich:}\\ Q=\frac{9\pi \cdot d(v_1+v_2)}{2U}\sqrt{\frac{{\eta }^3(v_2-v_1)}{\rho \cdot g}}\end{array}$
Durch Messung der Spannung U sowie der beiden Geschwindigkeiten lässt sich die Ladung bestimmen. Die übrigen Größen in der Gleichung sind Stoffkonstanten bzw. ergeben sich aus dem Versuchsaufbau (Abstand der Platten d). Bei den Experimenten ergab sich: Die Ladungen der Tröpfchen häuften sich bei ganzzahligen Vielfachen der Ladung $e=\text{1}\text{,602 176 46}\cdot {10}^{\text{-19}}\text{C}$
Das ist genau der Betrag der Elementarladung.