Physikalische Gesetze
In Erscheinungen der Natur und Technik kann man durch Beobachtungen oder Experimente, aber auch durch theoretische Überlegungen Zusammenhänge zwischen einzelnen Eigenschaften von Körpern, Stoffen oder Vorgängen erkennen. Wenn sich diese Zusammenhänge unter bestimmten Bedingungen immer wieder einstellen und für eine ganze Gruppe von Objekten gelten, dann spricht man von gesetzmäßigen Zusammenhängen, Gesetzmäßigkeiten oder Gesetzen.
Gesetze in der Physik sind allgemeine und wesentliche Zusammenhänge in Natur und Technik, die unter bestimmten Bedingungen stets wirken.
Das Wesen physikalischer Gesetze
Eingeschränkt auf den Bereich der Physik nennt man sie auch physikalische Gesetze.
Dabei ist der Weg bis zur Erkenntnis eines Gesetzes, so wie wir es heute kennen, in der Geschichte häufig langwierig und keineswegs geradlinig verlaufen.
Beispiel: Überlegungen zu den Kräften, die zwischen Körpern aufgrund ihrer Massen wirken, machten sich im 17. Jahrhundert verschiedene Wissenschaftler. ISAAC NEWTON (1643-1727) fand nach jahrelangen Untersuchungen mithilfe seiner berühmten Mondrechnung heraus, dass die Kraft zwischen zwei Körpern von ihrem Abstand abhängt und gab den folgenden Zusammenhang an:
In seiner heutigen Form lautet das Gesetz:
mit G als Gravitationskonstante, m und M als Massen der beiden Körper und r als Abstand ihrer Massenmittelpunkte. Die Gravitationskonstante konnte erstmals 1798 von HENRY CAVENDISH (1731-1810) mit einer Drehwaage bestimmt werden. Erst damit war das Gesetz in der angegebenen Form anwendbar.
Allgemein gilt:
| Gesetze in der Physik sind allgemeine und wesentliche Zusammenhänge in der Natur, die unter bestimmten Bedingungen stets wirken. Sie bestehen in der Regel aus Bedingungs- und Gesetzesaussagen. |
Die Gesetzesaussage ist beim Gravitationsgesetz die oben genannte Gleichung. Die Bedingungsaussagen, auch Gültigkeitsbedingungen oder Wirkungsbedingungen genannt, umfassen alle (bekannten) Bedingungen unter denen ein Gesetz wirkt. Diese werden häufig nicht explizite formuliert, weil man sie für selbstverständlich hält oder aus dem Zusammenhang erschließen kann. Mitunter sind auch nicht alle Wirkungsbedingungen bekannt. Beim Gravitationsgesetz besteht eine wichtige Bedingung der Anwendbarkeit darin, dass man die Körper als Massepunkte ansehen und damit den Abstand r angeben kann.
Dass Bedingungen mitunter nicht formuliert, aber trotzdem beachtet werden müssen, zeigen die folgenden Beispiele:
Beispiel 1: Für den Widerstand eines metallischen Leiters gilt die Gleichung:
Bedingungen werden hier zumeist nicht angegeben. Für die Anwendung ist aber zu beachten, dass die Stoffkonstante , der spezifische elektrische Widerstand, für die meisten Metalle temperaturabhängig ist. In Tafelwerken wird in der Regel der Wert dieser Konstanten für 20 °C angegeben. Nutzt man diesen Wert, dann bezieht sich der berechnete elektrische Widerstand auf eine Temperatur von 20 °C. Will man den Widerstand bei anderer Temperatur berechnen, dann man man die Temperaturabhängigkeit des spezifischen elektrischen Widerstandes beachten.
Beispiel 2: Für die Addition zweier Geschwindigkeiten, die die gleiche Richtung haben, gilt:
u = u' + v (1)
Diese Aussagen gilt uneingeschränkt für den Bereich der klassischen Physik. Sie gilt nicht mehr für große Geschwindigkeiten nahe der Lichtgeschwindigkeit. Für diesen Bereich wäre die relativistische Addition von Geschwindigkeiten anzusetzen, die lautet:
Es ist leicht erkennbar, dass für kleine Geschwindigkeiten u', v in Gleichung (2) der Term
gegen null geht und damit die Gleichung (2) in die Gleichung (1) übergeht.
Grenzen der Anwendbarkeit von Gesetzen
Ob ein Gesetz bei einem gegebenen Sachverhalt angewendet werden kann, ist im Wesentlichen davon abhängig, ob seine Gültigkeitsbedingungen exakt oder zumindest näherungsweise erfüllt sein.
Beispiel 1: Ein herabfallender Stein wird durch den Luftwiderstand beeinflusst. Diese Beeinflussung ist aber in der Regel so gering, dass man die Gesetze des freien Falls anwenden kann, die exakt nur für das Vakuum gelten. Für einen mit noch nicht geöffnetem Fallschirm fallenden Fallschirmspringer dagegen sind die Gesetze des freien Falles bei längerer Fallzeit nicht anwendbar, weil der wirkende Luftwiderstand zu einer gleichförmigen Bewegung mit einer maximalen Geschwindigkeit von ca. 200 km/h führt.
Beispiel 2: Bei einem Diskuswurf wird die Bewegung des Diskus durch den Luftwiderstand erheblich beeinflusst. Die Gesetze des schrägen Wurfes sind demzufolge nur in grober Näherung anwendbar, d.h. zwischen eventuellen Berechnungen und der Realität treten erhebliche Abweichungen auf.
Man muss also häufig in Abhängigkeit von den gegebenen Bedingungen entscheiden, ob man ein Gesetz anwenden kann oder nicht. Auch die Anwendungsbreite eines Gesetzes hängt entscheidend von den Gültigkeitsbedingungen ab.
Qualitative und quantitative Gesetzesaussagen
Physikalische Gesetze können unterschiedlich genau erkannt und in verschiedener Weise formuliert werden. Gesetze kann man qualitativ, halbquantitativ oder quantitativ formulieren.
Qualitative Gesetze: Es gibt Gesetze, die nur beschreiben, unter welchen Bedingungen eine bestimmte Erscheinung in der Natur auftritt. Ein Beispiel für ein solches Gesetz, das nur eine qualitative Gesetzesaussage enthält, ist das Induktionsgesetz in seiner elementaren Form. Es wird in Worten formuliert und lautet:
| In einer Spule wird eine Spannung induziert, solange sich das von der Spule umfasste Magnetfeld ändert. |
Halbquantitative Gesetze: Es gibt auch Gesetze, die einen Zusammenhang zwischen Eigenschaften bzw. Größen in der Tendenz beschreiben. Sie enthalten eine halbquantitative Gesetzesaussage und werden häufig in der Form „je ... desto“ formuliert. Ein Beispiel ist die Volumenänderung von Körpern bei Temperaturänderung.
| Für alle Körper gilt unter der Bedingung, dass sie sich ausdehnen können: Je größer die Temperaturänderung eines Körpers ist, umso größer ist auch seine Volumenänderung. |
Quantitative Gesetze: Bei vielen Gesetzen in der Physik kann der Zusammenhang zwischen Eigenschaften bzw. Größen mathematisch exakt beschrieben werden. Sie enthalten eine quantitative Gesetzesaussage. Ein Beispiel dafür ist das Weg-Zeit-Gesetz für gleichmäßig beschleunigte Bewegungen:
| Unter der Bedingung, dass sich ein Körper gleichmäßig beschleunigt bewegt und darüber hinaus zum Zeitpunkt t = 0 eine Anfangsgeschwindigkeit besitzt, gilt: |
Ein Gesetz - unterschiedliche Formulierungen
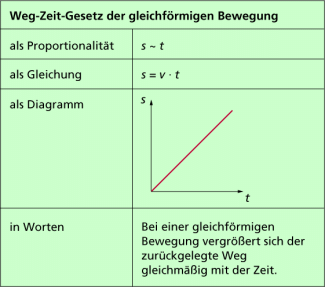
Eine quantitative Gesetzesaussage kann in Form einer Gleichung, aber auch in Worten, als Proportionalität oder in einem Diagramm dargestellt werden. Die unterschiedlichen Formulierungsmöglichkeiten sind in Bild 2 am Beispiel des Weg-Zeit-Gesetzes der gleichförmigen Bewegung dargestellt. Eine weitere Möglichkeit der Darstellung wäre die in Form einer Wertetabelle.
Dynamische und statistische Gesetze
In der Physik kann man zwischen dynamischen und statistischen Gesetzen unterscheiden.
Dynamische Gesetze geben an, wie sich ein Objekt unter gegebenen Bedingungen notwendig verhält. Ein Beispiel für ein dynamisches Gesetz ist das newtonsche Grundgesetz:
Kennt man die Kraft und die Masse eines Körpers, so kann man eindeutig sagen, welche Beschleunigung ihm erteilt wird. Die meisten in der Schule behandelten Gesetze sind solche dynamischen Gesetze.
Statistische Gesetze beschreiben dagegen das Verhalten einer großen Anzahl von Objekten, z.B. von Teilchen. Ein Beispiel dafür ist das Zerfallsgesetz des radioaktiven Zerfalls von Atomkernen. Es lautet:
Dieses Zerfallsgesetz beschreibt eindeutig, wie sich die Gesamtheit der Teilchen verhält. So kann man eindeutig voraussagen, dass nach einer Halbwertszeit genau die Hälfte der Atomkerne eines radioaktiven Stoffs zerfallen sind. Keine Aussage ist aber darüber möglich, ob das einen bestimmten Atomkern betrifft oder nicht. Das Gesetz trägt statistischen Charakter. Man bezeichnet deshalb solche Gesetze, die Aussagen über eine große Teilchenzahl machen, als statistische Gesetze.
Erfahrungssätze und Erhaltungssätze
Manche physikalischen Gesetze haben sich im Laufe der Entwicklung aus den Erfahrungen der Menschen über Zusammenhänge zwischen physikalischen Größen in der Natur ergeben. Es sind Gesetze, die nicht aus anderen Gesetzen hergeleitet und nur aus der Erfahrung heraus bestätigt werden.
Beispiele für solche Erfahrungssätze sind das Wechselwirkungsgesetz, der Energieerhaltungssatz oder die Hauptsätze der Wärmelehre.
Manche physikalische Größen haben in einem abgeschlossenen System einen bestimmten, konstanten Wert. Es sind Erhaltungsgrößen. Die Konstanz einer physikalischen Größe in einem abgeschlossenen System wird auch in Form von Gesetzen formuliert, die man als Erhaltungssätze oder als Gesetz von der Erhaltung ... bezeichnet.
Beispiele dafür ist der Energieerhaltungssatz, das Gesetz von der Erhaltung der Ladung, der Impulserhaltungssatz oder der Drehimpulserhaltungssatz..
Gesetze und ihre Bedeutung
Physikalische Gesetze existieren unabhängig vom Willen und von den Wünschen der Menschen. Wir können Gesetze zwar erkennen, können sie aber nicht verändern und schon gar nicht „überlisten“. Sie wirken unter den gegebenen Bedingungen, ob wir es wollen oder nicht.
Der Mensch kann aber Gesetze zu seinem Vorteil nutzen. So kann man das Hebelgesetz z. B. nutzen, um mit einem Flaschenöffner eine Flasche zu öffnen oder um mit einem Schraubenschlüssel eine Mutter anzuziehen. Dazu muss man das Gesetz noch nicht einmal kennen.
Physikalische Gesetze kann man auch nutzen, um technische Geräte zu bauen. So wird z. B. das Induktionsgesetz in Generatoren genutzt, um elektrische Energie zu gewinnen. Es wird auch genutzt, um Induktionsherde für den Haushalt herzustellen, bei denen sich die Stellfläche kaum noch erwärmt. Menschen können allerdings auch zu Schaden kommen, wenn sie das Wirken physikalischer Gesetze nicht beachten. Bei Unfällen mit Fahrzeugen kann das Wirken des Trägheitsgesetzes zu schwersten Schäden führen, wenn sich die Insassen nicht mit Sicherheitsgurten anschnallen oder wenn schwere Gegenstände auf der hinteren Ablage liegen. Erhebliche Probleme kann es auch geben, wenn Fahrzeugführer nicht beachten, dass bei nassen Straßen die Reibungskräfte viel geringer sind als bei trockenen Straßen. Dabei ist zu beachten: Auch bei Nutzung modernster Technik lassen sich physikalsiche Gesetze nicht „überlisten“.
Zum Teil treten auch Schäden für den Menschen und seine Umwelt deshalb auf, weil Gesetze oder ihre Gültigkeitsbedingungen noch nicht genau bekannt sind. Deshalb ist es ein wesentliches Ziel der Physik, Gesetze und Zusammenhänge immer genauer zu erkennen und zum Wohl des Menschen und seiner Umwelt zu nutzen.
Mithilfe von Gesetzen ist es möglich, Erscheinungen in Natur und Technik zu erklären und Voraussagen zu treffen, z.B. dazu, welche Beschleunigung ein Auto erreicht, wenn eine bestimmte Antriebskraft wirkt.
Nutzung von Gesetzen zum Erklären und Voraussagen
Gesetze können genutzt werden, um Sachverhalte in Natur, Technik und Alltag zu erklären oder voraussagen. So kann man z.B. die Gesetze der Optik nutzen, um die Entstehung eines Regenbogens oder die blaue Farbe des Himmels zu erklären.
Mithilfe der Gesetze der Wellenausbreitung kann die Orientierung von Fledermäusen erklärt werden. Die Strahlungsgesetze ermöglichen eine Erklärung dafür, warum Sterne unterschiedliche Farben haben.
Gesetze können auch genutzt werden, um Erscheinungen oder Werte von Größen vorherzusagen. So kann man z.B. vorhersagen, dass sich der Widerstand eines metallischen Leiters bei Temperaturerhöhung unter sonst gleichen Bedingungen vergrößert. Man kann auch angeben, wie groß die Stromstärke durch ein Bauelemente sein wird, wenn man (bei bekanntem Widerstand) eine bestimmte Spannung anlegt.
Welchen Wahrheitswert Erklärungen und Voraussagen haben, hängt entscheidend davon ab, ob alle Bedingungen erfasst und beachtet sind und welche Näherungen eingeflossen sind.
-
Ein Gesetz kann in unterschiedlicher Weise dargestellt werden.
Suche nach passenden Schlagwörtern
- qualitative Gesetzesaussage
- Wahrheitswert
- Gesetzesaussage
- Gesetzmäßigkeit
- Voraussagen
- Wirkungsbedingungen
- halbquantitative Gesetzesaussage
- Gültigkeitsbedingungen
- physikalische Gesetze
- Bedingungsaussage
- quantitative Gesetzesaussage
- Anwendbarkeit von Gesetzes
- Erhaltungssätze
- Erfahrungssätze
- statistische Gesetze
- Erhaltungsgrößen
- Anwendungsbreite von Gesetze
- dynamische Gesetze
- Erklären
- gesetzmäßiger Zusammenhang

