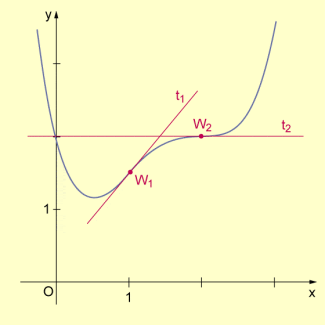
Krümmung und Wendepunkt

Durchfährt ein Rennfahrer beispielsweise die Grand-Prix-Strecke des Eurospeedway Lausitz, so muss er seinen Wagen durch eine Vielzahl von Links- und Rechtskurven mit dazwischenliegenden „Wendestellen“ lenken.

Die Graphen monotoner Funktionen kann man in ähnlicher Weise auf ihr sogenanntes Krümmungsverhalten bzw. auf Wendestellen untersuchen.

Kim hat in Deutsch, Mathe, Englisch und 6 weiteren Schulfächern immer eine von Lehrkräften geprüfte Erklärung, Video oder Übung parat.
24/7 auf Learnattack.de und WhatsApp mit Bildupload und Sprachnachrichten verfügbar. Ideal, um bei den Hausaufgaben und beim Lernen von Fremdsprachen zu unterstützen.
Viel günstiger als andere Nachhilfe und schützt deine Daten.

Jetzt 30 Tage risikofrei testen

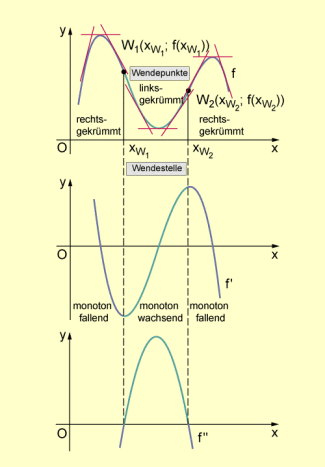
Anhand der grafischen Darstellung der Funktion sowie ihrer 1. und 2. Ableitung erkennt man für die Art der Krümmung folgende typischen Eigenschaften:

	Rechtsgekrümmte Kurvenstücke	Linksgekrümmte Kurvenstücke
Alle Tangenten an den Graphen in diesem Bereich liegen ...	... oberhalb des Graphen.	... unterhalb des Graphen.
Mit wachsenden x- Werten werden die Tangentenanstiege ...	... immer kleiner.	... immer größer.
Die erste Ableitung ist in diesem Intervall ...	... streng monoton fallend.	... streng monoton wachsend.
Die zweite Ableitung in diesem Intervall ...	... ist kleiner als null.	... ist größer als null.

An der Wendestelle $x_{w}$ bzw. dem zugehörigen Wendepunkt $W (x_{w}; f (x_{w}))$ ändert der Graph sein Krümmungsverhalten.

Tritt bei dem Graphen von f ein Wechsel von rechtsgekrümmt nach linksgekrümmt auf, so hat die 1. Ableitung von f in der Wendestelle $x_{w}$ ein lokales Minimum.

Erfolgt jedoch der Wechsel von links- nach rechtsgekrümmt, so hat die 1. Ableitung entsprechend ein lokales Maximum.

Verallgemeinert man diese Aussage, so ist eine Wendestelle dadurch gekennzeichnet, dass die 1. Ableitung an dieser Stelle ein Extremum haben muss.
Mögliche Wendestellen liegen also immer an denjenigen Stellen vor, an denen die 2. Ableitung Nullstellen besitzt.

Für die Existenz einer Wendestelle gilt folgende hinreichende Bedingung:

Eine Funktion f sei in ihrem Definitionsbereich dreimal differenzierbar.
Gilt für eine Stelle $x_{w}$ des Definitionsbereiches $f^{″} (x_{w}) = 0 u n d f^{‴} (x_{w}) \neq 0,$ so hat f an der Stelle $x_{w}$ eine Wendestelle.

Es gibt Wendestellen $x_{w},$ für die außerdem $f^{'} (x_{w}) = 0$ gilt, wo also die Tangente an den Graphen von f parallel zur x-Achse verläuft. Man nennt solche Wendepunkte Sattelpunkte, Terrassenpunkte oder Horizontalwendepunkte.

Unter einer Wendetangente versteht man diejenige Tangente, die den Graphen von f in ihrem Wendepunkt durchsetzt und somit die Kurventeile mit unterschiedlichem Krümmungssinn voneinander trennt.

Im folgenden Beispiel soll das Vorgehen bei der Untersuchung des Krümmungsverhaltens eines Funktionsgraphen gezeigt werden:

Beispiel: $f (x) = \frac{1}{2} x^{4} - 3 x^{3} + 6 x^{2} - 4 x + 2$

Bilden der ersten drei Ableitungen:
$\begin{array}{l} f^{'} (x) = 2 x^{3} - 9 x^{2} + 12 x - 4 \\ f^{″} (x) = 6 x^{2} - 18 x + 12 \\ f^{‴} (x) = 12 x - 18 \end{array}$

Die Nullstellen der 2. Ableitung erhält man aus $0 = 6 x^{2} - 18 x + 12 z u x_{1} = 1 u n d x_{2} = 2.$
Da $f^{‴} (1) = - 6 \neq 0 u n d f^{‴} (2) = 6 \neq 0$ ist, existieren bei $x_{1} u n d x_{2}$ tatsächlich Wendestellen.

Die Wendepunkte erhält man, indem die Wendestellen in die Ausgangsgleichung eingesetzt werden:
$\begin{array}{l} f (1) = 1,5 \Rightarrow W_{1} (1; 1,5) \\ f (2) = 2 \Rightarrow W_{2} (2; 2) \end{array}$

Für die Anstiege der Wendetangenten gilt:
$m_{1} = f^{'} (1) = 1 u n d m_{2} = f^{'} (2) = 0$
(Da der Anstieg des Graphen an der Wendestelle $x_{2}$ gleich null ist, ist $W_{2}$ ein Sattelpunkt.)

Nach Einsetzen der Koordinaten der Wendepunkte und des Anstiegs in die Geradengleichung $y = m x + n$ erhält man die Gleichungen für die Wendetangenten:
$\begin{array}{l} t_{1} : y = 1 x + 0,5 \\ t_{2} : y = 2 \end{array}$

Lernhelfer (Duden Learnattack GmbH): "Krümmung und Wendepunkt." In: Lernhelfer (Duden Learnattack GmbH). URL: http://www.lernhelfer.de/index.php/schuelerlexikon/mathematik-abitur/artikel/kruemmung-und-wendepunkt (Abgerufen: 30. June 2025, 11:32 UTC)

Suche nach passenden Schlagwörtern

Jetzt durchstarten

Entspannt durch die Schule mit KI-Tutor Kim und Duden Learnattack.

Kim hat in Deutsch, Mathe, Englisch und 6 weiteren Schulfächern immer eine von Lehrkräften geprüfte Erklärung, Video oder Übung parat.
24/7 auf Learnattack.de und WhatsApp mit Bildupload und Sprachnachrichten verfügbar. Ideal, um bei den Hausaufgaben und beim Lernen von Fremdsprachen zu unterstützen.
Viel günstiger als andere Nachhilfe und schützt deine Daten.

Verwandte Artikel

Sir Isaac Newton

* 04. Januar 1643 Woolsthorpe
† 20./21. März 1727 London

ISAAC NEWTON gilt als Begründer der klassischen Mechanik. Er entdeckte das Gravitationsgesetz sowie die nach ihm benannten newtonschen Axiome (Trägheitsgesetz, Grundgesetz der Mechanik und Wechselwirkungsprinzip).
NEWTON formulierte – etwa zur gleichen Zeit wie der deutsche Gelehrte GOTTFRIED WILHELM LEIBNIZ (1646 bis 1716) und unabhängig von diesem – Grundthesen der Infinitesimalrechnung. Insbesondere arbeitete er den Zusammenhang von Differenzieren und Integrieren heraus.

Monotonieverhalten von Funktionen

Im Folgenden soll der Zusammenhang zwischen Monotonie und 1. Ableitung untersucht werden.

Ableitung einer Funktion

Existiert an der Stelle $x_{0}$ des Definitionsbereiches einer Funktion f der Grenzwert
$\lim_{h \to 0} \frac{f (x_{0} + h) - f (x_{0})}{h}$ ,
so wird dieser als Ableitung oder Differenzialquotient von f an der Stelle $x_{0}$ bezeichnet.
Die Ableitung gibt den Anstieg des Funktionsgraphen an der Stelle $x_{0}$ an.

Ableitungen höherer Ordnung

Höhere Ableitungen einer Funktion f gestatten Rückschlüsse auf den Verlauf des Funktionsgraphen.
Ein Beispiel praktischer Anwendung höherer Ableitungen stellt die Untersuchung von Bewegungsabläufen in der Physik (etwa der Anfahrfunktion eines Kraftfahrzeuges) dar. Geschwindigkeit und Beschleunigung sind hier als erste bzw. zweite Ableitung des Weges nach der Zeit definiert.

Partielle Ableitungen

Für eine Funktion mit einer Gleichung $y = f (x)$ , also für eine Funktion mit genau einer unabhängigen Variablen x, ist die erste Ableitung $y' = f' (x_{0})$ an einer Stelle $x_{0}$ erklärt durch den Grenzwert des Differenzenquotienten an dieser Stelle:
$f' (x_{0}) = \lim_{h \to 0} \frac{f (x_{0} + h) - f (x_{0})}{h}$

Interpretiert man diesen Grenzwert geometrisch, so gibt er den Anstieg der Tangente an den Graphen von f im Punkte $P_{0} (x_{0}; f (x_{0}))$ an.

Es sei nun $z = f (x, y)$ die Gleichung einer Funktion f mit zwei unabhängigen Variablen x und y. Betrachtet man diese Funktion für ein konstantes $y = y_{0}$ , so erhält man eine Funktion $z = f (x, y_{0})$ mit nunmehr nur einer unabhängigen Variablen x, für die man wie oben angegeben den Grenzwert des Differenzenquotienten an einer Stelle $x_{0}$ aufstellen kann. Existiert dieser Grenzwert, so nennt man ihn die partielle Ableitung erster Ordnung der Ausgangsfunktion $z = f (x, y)$ nach x an der Stelle $(x_{0}; y_{0})$ und schreibt:
$f_{x} (x_{0}; y_{0}) = \lim_{h \to 0} \frac{f (x_{0} + h, y_{0}) - f (x_{0}, y_{0})}{h}$

Krümmung und Wendepunkt

Schule wird easy mit KI-Tutor Kim und Duden Learnattack

Suche nach passenden Schlagwörtern