Mittelpunkt einer Strecke
Eine Strecke sei durch die Koordinaten ihrer Endpunkte und (in der Ebene) bzw. und (im Raum) gegeben.
Um die Koordinaten des Mittelpunkts dieser Strecke zu bestimmen, kann man – und darin besteht ein Vorzug vektorieller Arbeitsweise – die Betrachtungen für die Ebene und den Raum zunächst einheitlich durchführen.
In beiden Fällen werden die Punkte durch ihre Ortsvektoren (bezüglich O, dem Koordinatenursprung) beschrieben.
Wir berechnen nun zunächst den Ortsvektor des Mittelpunktes M. Entsprechend der folgenden Abbildung gilt:
-
Mittelpunkt einer Strecke
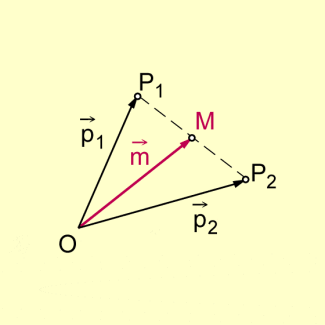
Die Gleichung ist die vektorielle Mittelpunktsgleichung, gültig für die Ebene und den Raum.
Unter Verwendung der Koordinaten der Ortsvektoren folgt hieraus im ebenen Fall, also mit
und
für die Koordinaten des Vektors :
Der Koordinatenvergleich ergibt die folgende Koordinatendarstellung:
Für den räumlichen Fall erhält man die dritte Koordinate analog. Hier gilt mit
und
, woraus man erhält.
Zusammenfassung
Für den Mittelpunkt M der Strecke
- in der Ebene mit den Endpunkten und gilt
- im Raum mit den Endpunkten und gilt
.
Die oben dargestellte Vorgehensweise ist ebenso anwendbar, wenn nicht die Koordinaten des Mittelpunkts einer Strecke zu ermitteln sind, sondern z.B. die Koordinaten eines Punktes, der diese Strecke im Verhältnis teilen soll.
-
Teilungspunkt einer Strecke
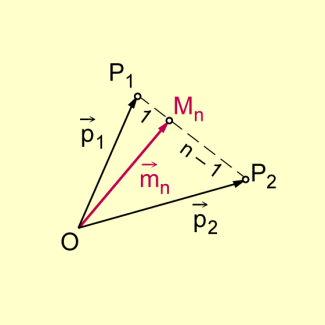
Wir bestimmen in diesem Fall der beliebigen Teilung einer Streckeden Vektor mit
.
Für den Halbierungspunkt, also für n = 2, erhält man als Spezialfall wieder das oben angeführte Resultat.

