Adam Ries

Zu einigen Lebensdaten

ADAM RIES (auch RIESE) wurde 1492 – also im Jahr der Entdeckung Amerikas durch Columbus – in Staffelstein (in Franken, nördlich von Bamberg) geboren. Die Familie war recht wohlhabend. Sein Vater besaß eine Mühle, einen Weinberg und mehrere Grundstücke.
Mit 17 Jahren ging RIES nach Zwickau und begann dort, sich mit Mathematik zu befassen. Von 1518 an trat er in Erfurt als Rechenmeister „Adam Rieß von Staffelstein“ auf und ging 1523 nach Annaberg. Dort wirkte er als Buchhalter im Bergbau, z. T. als „Gegenschreiber“ (d. h. als Kontrolleur oder Rechnungsprüfer), arbeitete als Rechner für die Gemeinde und stellte z. B. „Brottabellen“ auf, aus denen die Bäcker entnehmen konnten, wie teuer sie ihre Waren in Abhängigkeit vom Gewicht und vom aktuellen Getreidepreis verkaufen konnten. Bald wurde er durch seine Tüchtigkeit, seine Gewissenhaftigkeit und seine Sachkenntnis über die Stadt hinaus bekannt und erhielt 1539 den Titel „Kurfürstlich sächsischer Hofarithmeticus“.
Dadurch wurde er selbst wohlhabend und konnte seine 10-köpfige Familie ohne Not ernähren. Er verstarb hoch geachtet am 30.3.1559 in Annaberg, wo man heute ein Denkmal von ihm findet.

Der Rechenmeister ADAM RIES

ADAM RIES war kein Mathematiker in engerem Sinne, er hat keine mathematischen Zusammenhänge oder Gesetze gefunden. Sein Verdienst ist es viel mehr, weiten Kreisen seiner Zeitgenossen und Nachkommen den Zugang zu dieser Wissenschaft, vor allem zur Arithmetik eröffnet zu haben, und das zu einer Zeit, in der das, was heute in der Grundschule gelehrt wird, Stoff der Universitäten war. Er war damit der erste bedeutende Mathematiklehrer in Deutschland, und sein Name ist in der Redewendung „nach Adam Riese“ sprichwörtlich geworden.
Neben seiner beruflichen Tätigkeit leitete er eine Rechenschule, in der junge Menschen mathematisch gebildet wurden. Vor allem aber wirkte er durch seine Schriften, die dank ihres klaren Aufbaus, ihrer vorzüglich didaktischen Gestaltung und der Tatsache, dass sie sämtlich in deutscher Sprache verfasst waren, viel Anklang und weite Verbreitung fanden, sodass sie über Jahrzehnte hinaus als Lehrbücher verwendet wurden.

Dabei hat er sich neben vielem anderen vor allem um zwei Dinge verdient gemacht:

1. Er führte das schriftliche Rechnen und die dazu geeigneten Verfahren ein.
2. Er trug entscheidend dazu bei, dass die beim Rechnen umständlich zu benutzenden römischen Zahlen durch die arabischen Ziffern abgelöst wurden.

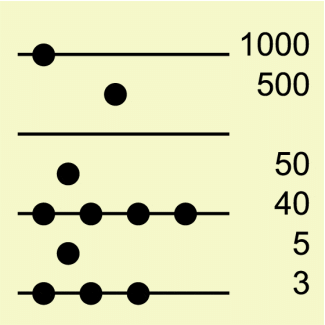
Zur damaligen Zeit rechnete man vor allem auf Rechenbrettern, die Abakus genannt wurden, oder einfach auf Tafeln, auf denen Linien gezogen waren. Die Zahlen wurden durch „Rechenpfennige“ oder Plättchen markiert. Wohlhabende Bürger benutzten eigens dafür (oft aus Silber) angefertigte Rechenpfennige. (Auf einem noch erhaltenen Rechenpfennig ist neben dem Annaberger Stadtwappen der folgende Spruch eingeprägt: Zwiespalt. Groszes. Gut. Verzehrt. Einigkeit. Das. Wenge. Mehrt, den man ADAM RIES zuschreibt.) Die Linien bezeichneten von unten nach oben die Stellenwerte Einer, Zehner usw., die Zwischenräume jeweils die Fünffachen. Die Grafik zeigt die Darstellung der Zahl 1598.

Durch Zulegen und „Umtausch“ der Plättchen wurde z. B. das Addieren ausgeführt. In seiner 1518 erschienen Schrift „Rechnen auf der Linihen“ zeigt RIES, wie auf dem Rechenbrett die verschiedenen Operationen ausgeführt werden. 1524 veröffentlicht er dann das Büchlein „Rechnung auf der Linihen und Federn“, in dem er die Verfahren des schriftlichen Rechnens darlegt, seine Vorteile zeigt und beide Methoden gegenüberstellt. Dabei waren viele Vorurteile zu überwinden (z. B. meinte man, diese Ziffern seien leichter zu fälschen), aber schließlich wurden doch die Vorzüge dieser Rechenart sichtbar.
1524 erschien von RIES verfasst ein umfassendes Lehrbuch der Arithmetik und Algebra, die sogenannte „Coß“. (Diese Bezeichnung kommt von dem italienischen Wort cosa, was „Sache“ oder „Ding“ bedeutet. Das Wort wurde von den italienischen Mathematikern zur Bezeichnung unbekannter Größen benutzt. Die Verfasser von Rechenbüchern nannte man danach „Cossisten“.) In seiner Coß beschreibt RIES neben der Darlegung von Rechenverfahren vor allem das Lösen von Aufgaben. Dazu werden ohne weitere Erläuterungen und Begründungen Vorschriften gegeben, Anleitungen also und zahlreiche Beispiele aus dem praktischen Leben. Dabei legte RIES Wert darauf, einfach zu schreiben, damit der arme Mann nicht übersetzt (überfordert, getäuscht) werde. Das Buch ist also gleichsam für ein Selbststudium gedacht.

In dem dargestellten Beispiel „Zech rechnen“ benutzt er sinngemäß folgenden Gedankengang:

Wären es nur Frauen, dann wären 63 Geldstücke ausgegeben worden. Es wurden aber 81 ausgegeben, also 18 mehr. Da jeder Mann 2 mehr ausgibt als jede Frau, müssen es 9 Männer, also 12 Frauen gewesen sein.

Grundsätzlich gibt er Anleitungen zum Überprüfen der Richtigkeit der Ergebnisse. Häufig verwendet er dabei die „Neunerprobe“. Sie beruht darauf, dass z. B. bei der Addition der Rest, den die Summe bei Division durch 9 lässt, sich aus der Addition der Reste der Summanden ergeben muss. Liegt dabei keine Übereinstimmung vor, wurde falsch gerechnet. (Die genannten Reste nennt RIES „prob“.) Diese Art der Prüfung von Ergebnissen ist auch bildhaft in seinem Wappen dargestellt.

Einige der von RIES dargestellten Verfahren sind bis heute fast unverändert übernommen worden, so z. B. das für die schriftliche Multiplikation. Andere mögen uns heute umständlich erscheinen, doch schuf ADAM RIES mit ihnen freie Bahn für die Nutzung des Rechnens und der Mathematik auch für die einfachen Menschen.