Exponentialgleichungen, Lösen

Exponentialgleichungen nennt man solche Gleichungen, in denen die Unbekannte im Exponenten auftritt.

1. Rechnerisches Lösen von Exponentialgleichungen

Exponentialgleichungen, in der nur Potenzen mit gleicher Basis auftreten oder unterschiedliche Basen auf die gleiche Basis zurückgeführt werden können, sind mithilfe der Anwendung der Potenzgesetze oder durch Logarithmieren lösbar.

Satz: Aus $a^x=a^y,a\ne \mathrm{0,}a\ne 1\text{ folgt x}=\text{y}$.

Beweis:
Es sei $a^x=a^y$ und x von y verschieden, etwa y = x + d. Dann folgt aus $a^x-a^y=0$ auch $a^x-a^{x+d}=0$ und nach Umformung:
$a^x\left(1-a^d\right)=0$
Weil $a\ne 0$ gilt, muss $1-a^d=0$ sein.
Das ist aber nur erfüllt für d = 0, also x = y.

Lösen von Exponentialgleichungen durch Exponentenvergleich

Beispiel 1:
      $\begin{array}{l}{49}^x=7^6\\ {\left(7^2\right)}^x=7^6\\ 7^{2x}=7^6\end{array}$
Daraus folgt 2x = 6, somit ist x = 3.

Beispiel 2:
       $\begin{array}{l}{5}^x=\sqrt[5]{5^2}\\ 5^x=5^{\frac{2}{5}}\end{array}$ 
Daraus folgt $x=\frac{2}{5}$.

Lösen von Exponentialgleichungen durch Logarithmieren

Lassen sich Exponentialgleichungen nicht auf einen Vergleich von Potenzen mit gleicher Basis zurückführen, so lassen sie sich manchmal durch Logarithmieren lösen.

Allgemeines Vorgehen:
$\begin{array}{l}{a}^x=b|\log arithmieren\\ \lg a^x=\lg b|Logarithmusgesetzanwenden\\ x\lg a=\lg b|:\lg a\\ x=\frac{\lg b}{\lg a}\end{array}$

Beispiel:
$\begin{array}{l}{5}^x=\mathrm{0,5}\\ x\lg 5=\lg \mathrm{0,5}\\ x=\frac{\lg \mathrm{0,5}}{\lg 5}=\frac{-\mathrm{0,301}}{\mathrm{0,69897}}=-\mathrm{0,43063}\end{array}$

2. Grafisches Lösen von Exponentialgleichungen

Einige Exponentialgleichungen lassen sich näherungsweise grafisch lösen. Dies bietet sich vor allem dann an, wenn die Variable nicht nur im Exponenten vorkommt, also keine reine Exponentialgleichung vorliegt.

Allgemeines Vorgehen:
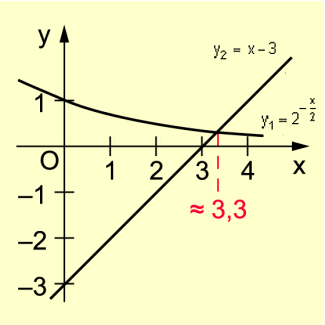
Die Gleichung wird so interpretiert, dass es sich um die Bestimmung des Schnittpunktes von zwei Funktionsgraphen handelt (Bild 1).

Beispiel:
$2^{-\frac{x}{2}}-x+3=0$
$y_1=2^{-\frac{x}{2}}{y}_2=x-3$

Die Werte zeigen, dass die Schnittstelle der Graphen zwischen
x = 3 und x = 3,3 liegen muss. Mit diesen Anfangswerten könnte nun ein Näherungsverfahren, z. B. Regula falsi, eingesetzt werden.