Logarithmusfunktionen
Funktionen mit Gleichungen der Form
heißen Logarithmusfunktionen.
Von besonderer Bedeutung sind die Logarithmusfunktionen mit den Basen 10 und 2 sowie der eulerschen Zahl e.
Der Zerfall von radioaktivem Jod-131 wird durch die Funktionsgleichung beschrieben. Dabei bedeuten die Ausgangsmasse und m(x) die vorhandene Masse nach x Tagen.
Will man ermitteln, nach wie vielen Tagen sich die Ausgangsmasse halbiert hat, so ist die Gleichung zu lösen, man muss also den Exponenten bei bekannter Basis und bekanntem Potenzwert bestimmen.
Es ist das Logarithmieren erforderlich:
Funktionen mit Gleichungen der Form
heißen Logarithmusfunktionen.
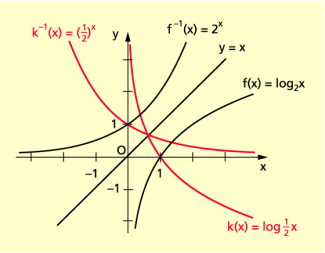
Die Logarithmusfunktion mit der Gleichung ist die Umkehrfunktion der Exponentialfunktion mit y = g(x) = (Bild 1).
-
Die Logarithmusfunktion y = f(x) = logax ist die Umkehrfunktion der Exponentialfunktion y = g(x) = ax
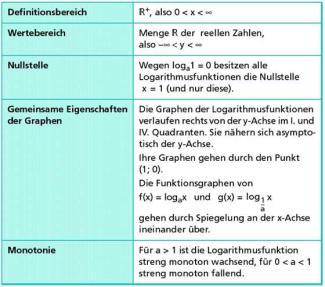
Logarithmusfunktionen besitzen die in Bild 2 aufgeführten Eigenschaften.
Von besonderer wissenschaftlicher und praktischer Bedeutung sind die Logarithmusfunktionen mit den Basen 10 und e sowie auch 2.
![]()
-
Eigenschaften der Logarithmusfunktionen
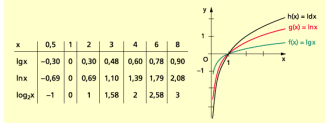
Man schreibt verkürzend:
Die Graphen der Funktionen sind in Bild 3 dargestellt.
-
Logarithmusfunktionen zur Basis 10, e und 2