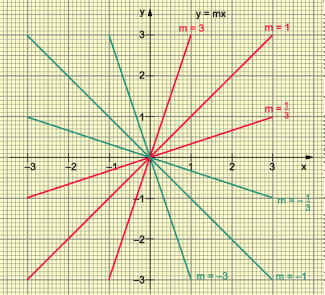
Funktionen mit der Gleichung y = mx
Jeder direkt proportionale Zusammenhang zwischen zwei Größen x und y kann durch eine spezielle lineare Funktion mit der Gleichung
beschrieben werden.
Definitonsbereich und Wertevorrat (Wertebereich) von f ist die Menge der reellen Zahlen . Der Graph von f ist eine Gerade, die durch den Koordinatenursprung O verläuft.
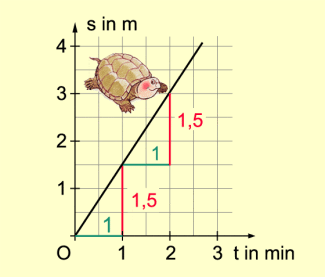
Wenn sich eine Schildkröte mit einer gleichbleibenden Geschwindigkeit von fortbewegt, so besteht zwischen zurückgelegtem Weg und verflossener Zeit ein spezieller funktionaler Zusammenhang: Es handelt sich um eine direkte Proportionalität mit dem Proportionalitätsfaktor . Mittels der Gleichung lässt sich der Weg berechnen, den die Schildkröte in der Zeit t (gemessen in Minuten) zurückgelegt hat.
| Zeit t in min | 0 | 1 | 2 | 3 | ... |
| Weg s in m | 0 | 1,5 | 3 | 4,5 | ... |
-
Weg-Zeit-Diagramm
Jeder direkt proportionale Zusammenhang zwischen zwei Größen y und x kann durch eine spezielle lineare Funktion mit der Gleichung y = f(x) = mx (m 0) beschrieben werden. Solche Funktionen haben folgende Eigenschaften:
- Der Definitions- und der Wertebereich ist .
- Der Graph von y = f(x) = mx ist stets eine Gerade, die durch den Koordinatenursprung verläuft.
Die Zahl m heißt dabei der Anstieg der Funktion f. Er gibt das Verhältnis einander zugeordneter Werte aus Definitions- und Wertebereich an.
-
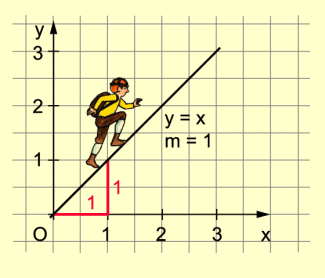
Steigende Gerade
-
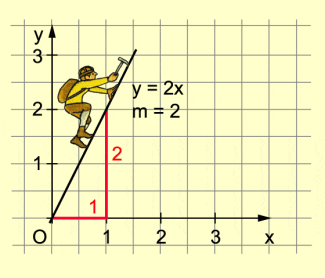
Steigende Gerade
Anschaulich betrachtet, kann man sagen:
Wenn x um 1 vergrößert wird, so verändert sich y um m.
Ist dabei m > 0, so wachsen die Funktionswerte an – die Gerade steigt.
Ist dagegen m < 0, so fallen die Funktionswerte wie auch die Gerade.
Um den Graphen einer linearen Funktion mit y = mx zu zeichnen, werden nur zwei Punkte benötigt. Als ein Punkt kann z.B. immer der Koordinatenursprung gewählt werden.
Einen zweiten Punkt erhält man, indem man
- die Koordinaten dieses Punktes mithilfe der Funktionsgleichung berechnet oder
- den Anstieg m benutzt.
-
Fallende Gerade
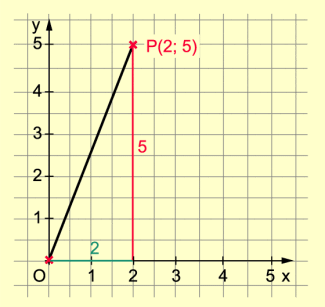
Beispiel 1: Koordinaten mittels Funktionsgleichung berechnen
Für :
:
-
y = 2,5x
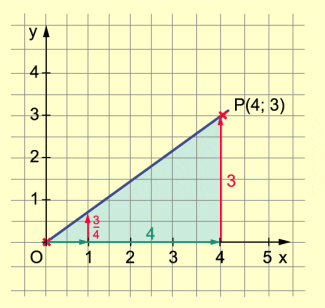
Beispiel 2: Koordinaten mittels Anstieg bestimmen
y = x; m =
Wenn x um 1 wächst, so wächst y um ,
wenn x um 4 wächst, wächst y um 3.
P (4; 3 )
-
y = 0,75x
Beispiel 3: y = – 2x
Für x = 1:
y = – 2 · 1
y = – 2
(1; – 2)
Oder:
Für x = – :
y = – 2 · (– )
y = 1
(– ; 1)
-
y = - 2x
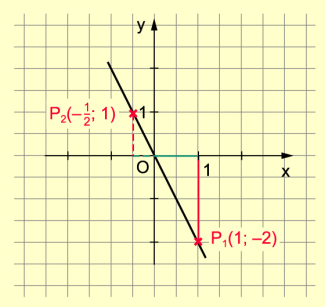
Beispiel 4: y = – x
m = –
Wenn x um 1 wächst, so fällt y um ,
wenn x um 2 wächst, so fällt y um 1.
Oder: Wenn x um 2 fällt, so wächst y um 1.
-
y = - 0,5x
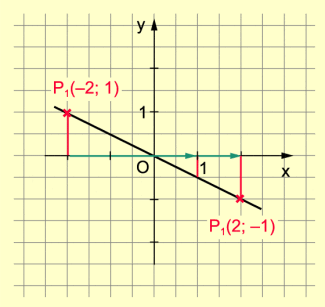
Das eingezeichnete rechtwinklige Dreieck nennt man Anstiegsdreieck (Steigungsdreick). Anstiegsdreiecke kann man in beliebiger Größe und an beliebiger Stelle zeichnen sowie entlang des Graphen verschieben.
-
Anstiegsdreieck
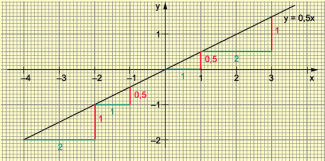
Durch die Gleichung y = f(x) = mx wird eine ganze Schar von Funktionen beschrieben, die sich nur im Anstieg m unterscheiden. Die Zahl m wird ein Parameter der Funktionsschar y = mx genannt. Zu der Funktionsschar gehört eine Geradenschar, deren einzelnen Elemente für m > 0 wachsen (steigen) und für m < 0 fallen.
-
Schar von Funktionen