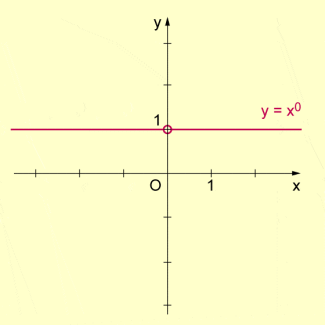Potenzfunktionen

Es ist zweckmäßig, eine Einteilung der Pozenzfunktionen in Abhängigkeit vom Exponenten n vorzunehmen.

Potenzfunktionen mit geraden Exponenten

Ist der Exponent n in $y=f\left(x\right)=x^n$ eine gerade Zahl $(n=2k$ mit $k\in \mathbb{Z})$, so liegen gerade Funktionen vor, d.h. die y-Achse ist Symmetrieachse für die Funktionsgraphen.

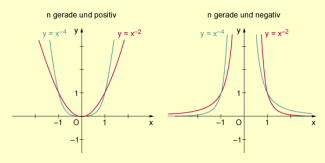
Weitere Eigenschaften dieser Funktionen sind im Folgenden zusammengestellt.

Potenzfunktionen mit ungeraden Exponenten

Ist der Exponent n in $y=f\left(x\right)=x^n$ eine gerade Zahl $(n=2k+1$ mit $k\in \mathbb{Z})$, so liegen ungerade Funktionen vor, d.h. die Funktionsgraphen sind punktsymmetrisch (zentralsymmetrisch) zum Koordinatenursprung O.

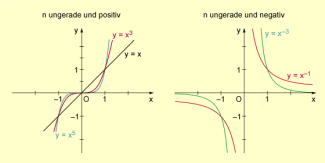
Weitere Eigenschaften dieser Funktionen sind im Folgenden zusammengestellt.

Die Graphen der Funktionen $y=f\left(x\right)=x^{-1},y=f\left(x\right)=x^{-2},\mathrm{...}$ heißen Hyperbeln ersten, zweiten, ... Grades. Sie bestehen jeweils aus zwei Teilen, den Hyperbelästen.

Eine Sonderstellung nimmt die Funktion $y=f\left(x\right)=x^n$ mit $n=0$ ein. Wegen $x^0=1$ und $x\ne 0$ hat die Funktion an der Stelle $x_1=0$ eine „Lücke“. Ihr Graph ist eine Parallele zur x-Achse im Abstand 1 mit Ausnahme des Punktes $P_1\left(0;1\right).$