Funktionen von mehreren Variablen

Unsere „gewöhnlichen“ Funktionen sind eindeutige Zuordnungen der Elemente einer „Definitionsmenge“ zu den Elementen einer „Wertemenge“. Die Elemente der Definitionsmenge sind reelle Zahlen, die Elemente der Wertemenge ebenfalls. Mit diesem Modell können wir viele interessante Vorgänge in Form einer Funktion beschreiben.
Es besteht aber eigentlich kein Grund, als Elemente von Definitions- bzw. Wertemenge nur reelle Zahlen zuzulassen. Wir könnten ebenso gut Zahlenpaare, Zahlentripel oder allgemein n-Tupel verwenden, wenn wir genau festlegen, wie wir damit umgehen wollen.

• Beispiel 1:
  Es sei ein Paar $(x;y)$ gegeben, dann gilt für den Flächeninhalt des Rechtecks mit den Seiten(längen) x und y:
  $A=x\cdot y$
• Beispiel 2:
  Es sei ein Tripel $(x;y;z)$ gegeben, dann gilt für das Volumen des von x, y und z aufgespannten Quaders:
  $V=x\cdot y\cdot z$
• Beispiel 3:
  Vier „Zahlen“ (Widerstände) $R_1,R_2,R_3,R_4$ sind gegeben, dann berechnen wir den Gesamtwiderstand bei Parallelschaltung nach dem ohmschen Gesetz wie folgt:
  $R={\left(\frac{1}{R_1}+\frac{1}{R_2}+\frac{1}{R_3}+\frac{1}{R_4}\right)}^{-1}$

Die einfachste Verallgemeinerung des Funktionsbegriffs erhalten wir für Funktionen von zwei (unabhängigen) Variablen:

• Definition: Es sei D eine Menge von (reellen) Zahlenpaaren $(x;y)$. Wird durch eine bestimmte Funktionsvorschrift f jedem Zahlenpaar $(x;y)\in D$ genau eine reelle Zahl z mit $z=f(x,y)$ zugeordnet, so heißt f eine (reellwertige) Funktion von den beiden Variablen x und y:
  $(x;y)\stackrel{f}{\to }z=f(x,y)\in R(\ast )$

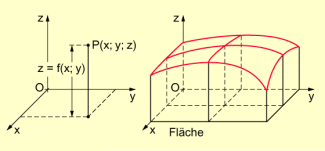
Gibt es auch zu Funktionen mit zwei Variablen grafische Darstellungen? Deutet man x und y als Koordinaten der xy-Ebene, dann stellt jedes Paar $(x;y)$ einen Punkt dieser Ebene dar. Diesem Punkt ist aber auf Grund der Funktionsgleichung $(\ast )$ genau ein Wert von z zugeordnet. Wenn man z als dritte Koordinate in dreidimensionalem Raum ${ℝ}^3$ auffasst, so erhält man als Funktionsgraphen eine Fläche im dreidimensionalem Raum. Jede Funktion $z=f(x,y)$ kann deshalb als Fläche in ${ℝ}^3$ dargestellt werden (siehe Abbildung).
Aber die Graphen von Funktionen von mehr als zwei Variablen kann man nicht mehr geschlossen zeichnen, d.h., eine geometrische Interpretation ist dann nicht mehr möglich!

Bestimmen Sie den Definitionsbereich D der folgenden Funktionen

• Beispiel 4:
  $z=f(x,y)=\sqrt{x-y}$
  Lösung: $x-y\ge 0\Rightarrow y\le x$
  D: alle Punkte mit der Eigenschaft $y\le x$
• Beispiel 5:
  $z=f(x,y)=\sqrt{x^2+y^2-1}+\ln (4-x^2-y^2)$
  Lösung: $1\le x^2+y^2<4$
  D: alle Punkte des Kreisringes ohne äußere Kreislinie

Weitere Beispiele für Funktionen von mehreren Variablen aus der Mathematik

1. Heronsche Formel für den Flächeninhalt des Dreiecks ABC
   $A=f(a,b,c)=\sqrt{s(s-a)(s-b)(s-c)}$ mit $s=\frac{1}{2}(a+b+c)$
2. Flächeninhalt des Dreiecks ABC
   $A=f(a,\beta ,\gamma )=\frac{1}{2}{a}^2\frac{\sin \beta \cdot \sin \gamma }{\sin (\beta +\gamma )}$
3. Flächeninhalt des Kreisringes
   $A=f(r_1,r_2)=\pi \left(r_2{}^2-r_1{}^2\right)$
4. Volumen des geraden Kreiszylinders
   $V=f(r,h)=\pi r^{2}h$
5. Volumen des geraden Hohlzylinders
   $V=f(r_1,r_2,h)=\pi h\left(r_2{}^2-r_1{}^2\right)$
6. Arithmetisches Mittel für n Zahlen $a_1,a_2,\mathrm{...,}{a}_n$
   $\overline{x}=f(a_1,a_2,\mathrm{...,}{a}_n)=\frac{a_1+a_2+\mathrm{...}+a_n}{n}$
7. Geometrisches Mittel für n positiven Zahlen $p_1,p_2,\mathrm{...,}{p}_n$
   $g=f(p_1,p_2,\mathrm{...,}{p}_n)=\sqrt{p_1\cdot p_2\cdot \mathrm{...}\cdot p_n}$
8. Harmonisches Mittel für n von null verschiedenen Zahlen
   $h=f(b_1,b_2,\mathrm{...,}{b}_n)=\frac{n}{\frac{1}{b_1}+\frac{1}{b_2}+\mathrm{...}\frac{1}{b_n}}$

Beispiele aus Physik und Technik

1. Newtonsches Gravitationsgesetz
   (Betrag der Kraft F, mit der sich zwei Massen $m_1,m_2$ mit dem Abstand r gegenseitig anziehen; $\gamma =\mathrm{6,673}\cdot {10}^{-11}N{m}^{2}k{g}^{-2}$ Gravitationskonstante)
   $F=f(m_1,m_2,r)=\gamma \cdot \frac{m_1\cdot m_2}{r^2}$
2. Gasgesetz für ideale Gase
   (p Druck, V Volumen, T absolute Temperatur, R allgemeine Gaskonstante)
   $p=f(T,V)=\frac{RT}{V};V=f(T,p)=\frac{RT}{p};T=f(p,V)=\frac{1}{R}pV$
3. Durchlässigkeit p der Panzerung für das Geschoss mit Durchmesser d, Gewicht G und Treffgeschwindigkeit v
   $p=f(G,v,d)=R\cdot \frac{G^{\frac{5}{7}}\cdot v^{\frac{10}{7}}}{d^{\mathrm{3,75}}}(R$ Konstante$)$
4. Potential $\varphi$ im Punkt P(x; y) des elektrostatischen Feldes zweier Punktladungen Q und $-Q$
   ( ${\epsilon }_0$Vakuum-Influenzkonstante)
   $\varphi =f(x,y)=\frac{Q}{4\pi {\epsilon }_0}\cdot \left(\frac{1}{\sqrt{{(a+x)}^2+y^2}}-\frac{1}{\sqrt{{(a-x)}^2+y^2}}\right)$

Beispiele aus der Wirtschaftswissenschaft

1. Jahresaufwendungen eines Betriebes
   $\begin{array}{l}f(x_1,x_2)=a+b_1{x}_1+b_2{x}_2+\frac{c_1}{x_1}+\frac{c_2}{x_2}\\ (a,b_1,b_2,c_1,c_2\text{ Konstanten})\end{array}$
2. Nutzenfunktion eines durchschnittlichen Vier-Personen-Haushaltes
   ( $x_1$ monatliche Nahrungsmittelausgaben in EUR/Monat, $x_2$ zur Verfügung stehende Wohnfläche in $m^2,x_3$ monatlicher Energieverbrauch in kWh/Monat, $x_4$ monatliche Ausgaben für Körperpflege in EUR/Monat)
   $U=f(x_1,x_2,x_3,x_4)=2000x_1+9760x_2+2x_2{x}_3+4x_1{x}_4$
3. COBB-DOUGLAS-Produktionsfunktion
   (mit x als Output und $r_k$ als Input des k-ten Faktors)
   $x=f(r_1,r_2,\mathrm{...,}{r}_n)=a_0\cdot r_1{}^{a_1}\cdot r_2{}^{a_2}\cdot \mathrm{...}\cdot r_n{}^{a_n}(a_0>0;r_k>0)$