Geraden am Kreis
Geraden und Kreise können verschiedene Lagen zueinander haben:
- Eine Gerade, die den Kreis in zwei Punkten schneidet, heißt Sekante (Schneidende). Eine Sekante, die durch den Mittelpunkt des Kreises verläuft, nennt man Zentrale.
- Die Strecke zwischen den Punkten A und B ist eine Sehne des Kreises. Die längste Sehne im Kreis ist der Durchmesser d.
- Eine Gerade, die den Kreis in einem Punkt berührt, heißt Tangente (Berührende).
- Eine Gerade, die den Kreis in keinem Punkt schneidet, heißt Passante (Vorbeigehende).
Geraden und Kreise können verschiedene Lagen zueinander haben (Bild 1).
- Eine Gerade, die den Kreis in zwei Punkten schneidet, heißt Sekante (Schneidende). Eine Sekante, die durch den Mittelpunkt des Kreises verläuft, nennt man Zentrale.
- Die Strecke zwischen den Punkten A und B ist eine Sehne des Kreises. Die längste Sehne im Kreis ist der Durchmesser d.
- Eine Gerade, die den Kreis in einem Punkt berührt, heißt Tangente (Berührende).
- Eine Gerade, die den Kreis in keinem Punkt schneidet, heißt Passante (Vorbeigehende).
Tangentenkonstruktionen
1. Konstruktion der Kreistangente in einem Punkt P des Kreises (Bild 2)
- Es wird die Strecke PM gezeichnet.
- In P wird die Senkrechte zu PM konstruiert.
2. Konstruktion der Tangenten von P an einen Kreis k (Bild 3)
- Die Strecke PM wird gezeichnet und halbiert.
- Um den Mittelpunkt T der Strecke PM wird ein Kreisbogen mit dem Radius gezeichnet.
- Die Schnittpunkte des Kreisbogens mit dem Kreis k sind die Berührungspunkte und der gesuchten Tangenten.
- Die Tangenten und werden gezeichnet.
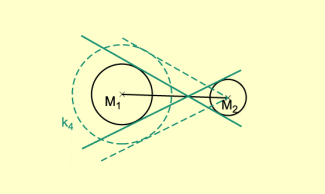
3. Konstruktion der gemeinsamen Tangenten an zwei sich nicht berührende und nicht ineinanderliegende Kreise
a) äußere Tangenten (Bild 4)
- Um wird ein Kreis mit dem Radius
( ) gezeichnet.- Es werden die Tangenten von an konstruiert.
- Durch Parallelverschiebung werden die außen liegenden Tangenten im Abstand konstruiert.
b) innere Tangenten (Bild 5)
- Um wird ein Kreis mit dem Radius
( ) gezeichnet.- Es werden die Tangenten von an konstruiert.
- Durch Parallelverschiebung werden die innenliegenden Tangenten im Abstand konstruiert.
-
Geraden und Kreis
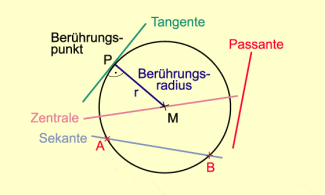
-
Konstruktion der Kreistangente
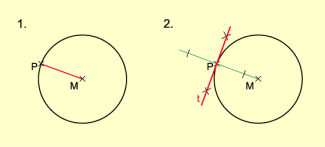
-
Konstruktion der Tangenten an einen Kreis
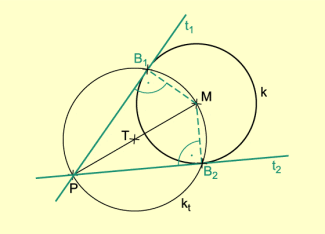
-
Konstruktion der äußeren Tangenten
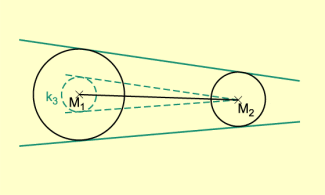
-
Konstruktion der inneren Tangenten
Lernhelfer (Duden Learnattack GmbH): "Geraden am Kreis." In: Lernhelfer (Duden Learnattack GmbH). URL: http://www.lernhelfer.de/index.php/schuelerlexikon/mathematik/artikel/geraden-am-kreis (Abgerufen: 23. February 2026, 10:46 UTC)

