Möndchen des Hippokrates

HIPPOKRATES VON CHIOS ( griechischer Mathematiker, um 440 v. Chr.) war der berühmteste Geometer des 5. Jh. v. Chr. Von ihm stammt nach Überlieferung die erste zusammenfassende Darstellung geometrischen Wissens seiner Zeit unter dem Titel „Elemente“ nach dem Schema Voraussetzung, Satz und Beweis. Darin verwendet er für die Bezeichnung geometrischer Figuren Buchstaben. Er beschrieb den Zusammenhang von Peripheriewinkel (Umfangswinkel) und Bogen, die Konstruktion des Sechsecks und des Umkreises des Dreiecks, Verallgemeinerungen des pythagoräischen Lehrsatzes für ähnliche Figuren über den Dreieckseiten sowie für das stumpfwinklige Dreieck. Er zeigte Umwandlungen von Polygonen in flächengleiche Quadrate.
Verdrängt wurde diese Darstellung durch die umfangreicheren späteren „Elemente“ des EUKLID. Doch dürfte der Inhalt der ersten vier Bücher der euklidischen „Elemente“ auf die Vorlage von HIPPOKRATES zurückgehen.
Eng verbunden ist der Name HIPPOKRATES auch mit zwei berühmten Problemen der Mathematik.

Die Quadratur des Kreises, die Umwandlung des Kreises in ein flächengleiches Quadrat

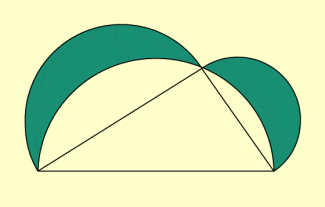
Die Quadratur des Kreises hatte keinen Erfolg, so versuchte man wenigstens von Kreisbogen begrenzte Flächen in flächengleiche Vielecke zu verwandeln. Am bekanntesten sind wohl die Möndchen des Hippokrates (Bild 3).
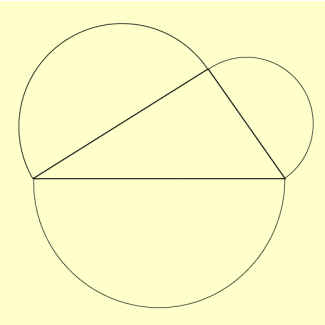
Über den Seiten des rechtwinkligen Dreiecks ABC werden Halbkreise gezeichnet (Bild 1). Nach dem Satz des Thales ist das Dreieck ABC rechtwinklig. Es gilt:
$a^2+b^2=c^2$
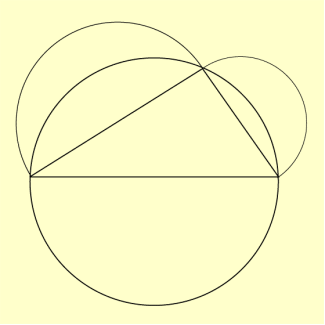
Durch Umklappung des Halbkreis es über c (Bild 2) entstehen sichelförmige Flächen, genannt „Möndchen“ (Bild 3). Für die Flächen der Halbkreise gilt nach dem Satz des Pythagoras:

$A{}_a=\frac{1}{8}\cdot \pi \cdot a^2$
Flächeninhalt des Halbkreises über der Seite a
$A{}_b=\frac{1}{8}\cdot \pi \cdot b^2$
Flächeninhalt des Halbkreises über der Seite b und
$A{}_c=\frac{1}{8}\cdot \pi \cdot c^2$
Flächeninhalt des Halbkreises über der Seite c und es gilt: $A{}_a+A{}_b=A{}_c$
Damit folgt für die Beziehung von Dreieck und Halbkreisen:$A{}_{\Delta }+A{}_a+A{}_b=A{}_M+A{}_c\Rightarrow A{}_{\Delta }=A{}_M$

In Worten: Die Summe der Flächeninhalte der beiden Möndchen ist dem Flächeninhalt des Dreiecks ABC gleich.

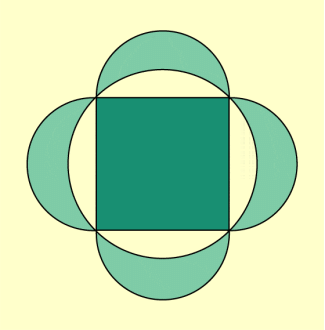
Betrachtet man die in gleicher Weise an einem Quadrat erzeugten Möndchen, zeigt sich ebenfalls eine Gleichheit der Summe der Flächeninhalte der vier Möndchen zum Flächeninhalt des Quadrates (Bild 4).
HIPPOKRATES fand fünf verschiedene Typen quadrierbarer Möndchen.
Diese Entdeckung ist in dem ältesten authentischen Dokument griechischer Mathematik teilweise überliefert, was ihre Bedeutung unterstreicht.
Durch diese Besonderheiten irre geleitet, versuchten viele Mathematiker vergeblich eine Quadratur des Kreises. Erst 1882 lieferte F. LINDEMANN (1852 bis 1939) den Beweis, dass eine Quadratur des Kreises nicht möglich ist.
Der Begriff „Quadratur des Kreises“ wird heute für unlösbare Aufgaben benutzt.

Die Verdopplung des Würfels oder das delische Problem

Es geht um die Konstruktion eines Würfels mit dem doppelten Volumen eines gegebenen Würfels, von der wir heute wissen, dass dies mit Zirkel und Lineal nicht möglich ist. HIPPOKRATES fand weitere zu diesem äquivalente Problemstellungen.