Grundkonstruktionen

Zu den Grundkonstruktionen in der Geometrie werden im Allgemeinen die folgenden mit Zirkel und Lineal auszuführenden Konstruktionen gezählt:

1. Halbieren einer Strecke (die Mittelsenkrechte errichten)
2. Halbieren eines Winkels (die Winkelhalbierende konstruieren)
3. Errichten der Senkrechten zu einer Geraden in einem Punkt der Geraden
4. Fällen des Lotes von einem Punkt auf eine Gerade

Die beiden elementaren Konstruktionen „Abtragen einer Strecke“ und „Antragen eines Winkels“ werden bei dieser Aufzählung vorausgesetzt.
Zu den Anwendungen der Grundkonstruktionen gehören u. a.:

• Konstruieren der Parallelen zu einer Geraden durch einen Punkt außerhalb der Geraden
• Konstruieren der Parallelen zu einer Geraden im vorgegebenen Abstand

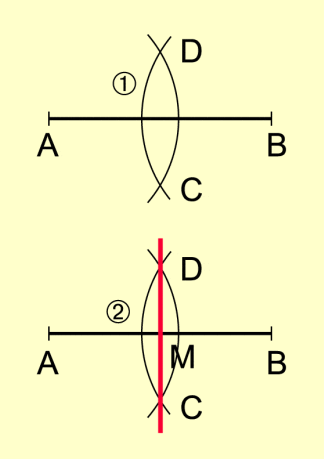
Halbieren einer Strecke

Konstruktionsbeschreibung:

1. Um A und B werden Kreisbögen mit beliebigem, aber gleichem Radius ( $r>\frac{1}{2}\overline{AB}$ ) gezeichnet.
   Diese Kreisbögen schneiden einander in C und D.
2. Die Gerade CD wird gezeichnet. Sie schneidet die Strecke AB in M.

Mithilfe dieser Konstruktion wird die Strecke AB halbiert. Der Punkt M ist der Mittelpunkt der Strecke AB (Bild 2).
Die Gerade CD ist die Mittelsenkrechte der Strecke AB.

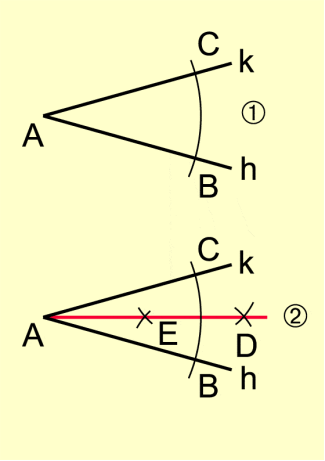
Halbieren eines Winkels

Konstruktionsbeschreibung:

1. Um den Scheitelpunkt A wird ein Kreisbogen gezeichnet. Er schneidet die Schenkel des Winkels $\sphericalangle$ (h, k) in den Punkten B und C (Bild 3).
2. Um B und C werden Kreisbögen mit beliebigem, aber gleichem Radius gezeichnet.
3. D und E sind die Schnittpunkte der beiden Kreisbögen. Der Strahl von A durch E und D wird gezeichnet. Er ist die Winkelhalbierende des Winkels $\sphericalangle$ (h, k).

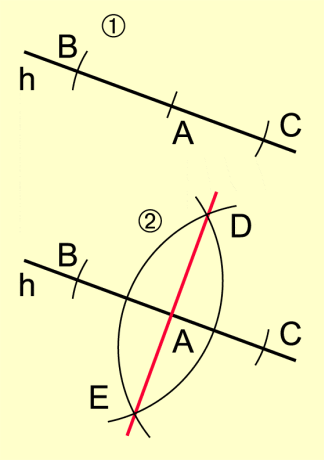
Errichten der Senkrechten in einem Punkt der Geraden

Konstruktionsbeschreibung:

1. Um A wird ein Kreisbogen gezeichnet. Er schneidet die Gerade h in den Punkten B und C.
2. Um B und C werden Kreisbögen mit beliebigem, aber gleichem Radius ( $r>\overline{AB}$ ) gezeichnet. Die Kreisbögen schneiden einander in den Punkten D und E. Die Gerade durch A, D und E wird gezeichnet. Sie ist die Senkrechte zu h in A (Bild 4).

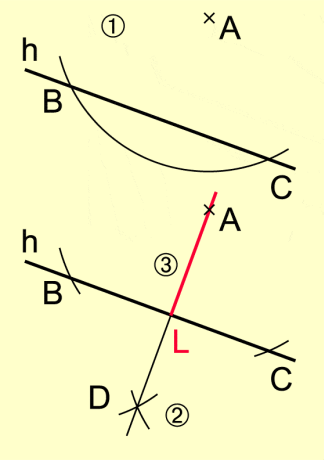
Fällen des Lots auf eine Gerade von einem Punkt außerhalb der Geraden

Konstruktionsbeschreibung:

1. Ein Kreisbogen um A wird gezeichnet, der die Gerade h in zwei verschiedenen Punkten B und C schneidet.
2. Um B und C werden Kreisbögen mit beliebigem, aber gleichem Radius ( $r>\frac{1}{2}\overline{BC}$ ) gezeichnet, die sich in D schneiden. Die Gerade AD schneidet die Gerade h im Punkt L.
3. Die Strecke AL ist das Lot von A auf die Gerade h. Der Punkt L heißt Lotfußpunkt (Bild 5).