Dreiteilung des Winkels

Die Trisektion (Dreiteilung) eines beliebigen Winkels nur mit Zirkel und Lineal gehört neben der Quadratur des Kreises und der Verdoppelung eines Würfels zu den bekanntesten geometrischen Problemen.

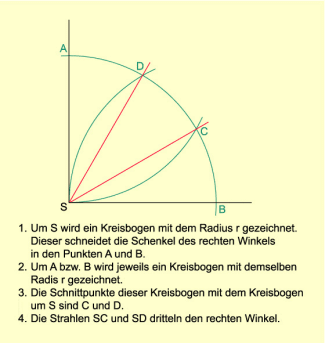
Es lässt sich mithilfe der Algebra nachweisen, dass die exakte Dreiteilung eines beliebigen Winkels nur mit Zirkel und Lineal nicht möglich ist. Dieser Nachweis ist 1837 PIERRE LAURENT WANTZEL (1814 bis 1848) gelungen.
Lediglich für spezielle Winkelgrößen ($45°$, $90°$, $180°$ usw.) ist diese Konstruktion ausführbar.

Bereits in der Antike gab es Versuche, die Dreiteilung eines beliebigen Winkels näherungsweise oder exakt mit weiteren Hilfsmitteln konstruktiv umzusetzen. So konstruierte PAPPOS VON ALEXANDRIA um 320 v. Chr. eine Näherungslösung, indem er eine Hyperbelkonstruktion nutzte.

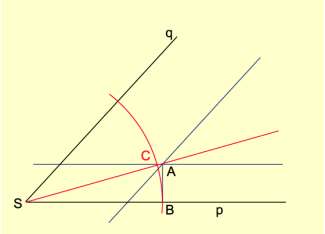
Eine gute Näherung stellt die folgende Konstruktion für Winkel $\left(\alpha <90°\right)$ dar (Bild 2):

Gegeben ist eine beliebiger Winkel (p; q) mit dem Scheitelpunkt S.
Man zeichnet zu p im Inneren des Winkels eine Parallele im Abstand a.
Man zeichnet zu q im Inneren des Winkels eine Parallele im Abstand 2a.
Vom Schnittpunkt A auf der Parallelen wird das Lot auf den Schenkel p gefällt. Der Lotfußpunkt ist B.
Um S wird ein Kreisbogen mit dem Radius $\overline{SB}$ gezeichnet. Der Schnittpunkt des Kreisbogens mit der Parallelen zu p ist C.
Der Schenkel des Winkels p und der Strahl SC bilden einen Winkel, dessen Größe etwa ein Drittel des Winkels (p; q) beträgt.

Mithilfe der Winkelbeziehungen am rechtwinkligen Dreieck kann man die Näherungskonstruktion numerisch prüfen.