Kongruenz von Dreiecken
Zwei Dreiecke sind zueinander kongruent, wenn es eine Bewegung gibt, die ein Dreieck auf das andere abbildet. Die beiden Dreiecke stimmen dann in allen sechs Bestimmungsstücken oder Maßen überein. Die Konstruktion eines Dreiecks ist möglich, wenn drei voneinander unabhängige Bestimmungsstücke gegeben sind. Daher wird auch bei der Betrachtung der Kongruenz von Dreiecken von drei Seiten oder Winkeln ausgegangen.
Zwei Dreiecke sind zueinander kongruent, wenn es eine Bewegung gibt, die ein Dreieck auf das andere abbildet. Die beiden Dreiecke stimmen dann in allen sechs Bestimmungsstücken oder Maßen überein (Bild 1). Die Konstruktion eines Dreiecks ist möglich, wenn drei voneinander unabhängige Bestimmungsstücke gegeben sind. Daher wird auch bei der Betrachtung der Kongruenz von Dreiecken von drei Seiten oder Winkeln ausgegangen.
-
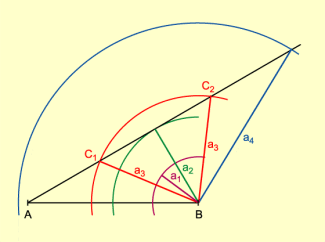
Kongruente Dreiecke

(c) Duden Learnattack
Kongruenzsatz sss
Zwei Dreiecke sind zueinander kongruent, wenn sie in allen drei Seiten übereinstimmen (Bild 2).
Es sind
also ist auch .
-
Kongruenzsatz sss
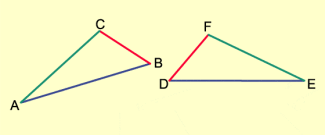
Kongruenzsatz sws
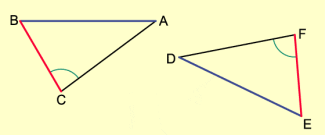
Zwei Dreiecke sind zueinander kongruent, wenn sie in zwei Seiten und dem eingeschlossenen Winkel übereinstimmen (Bild 3).
Es sind und ,
also ist auch .
-
Kongruenzsatz sws
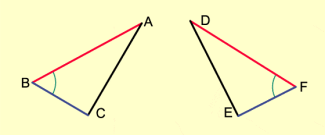
Kongruenzsatz wsw
Zwei Dreiecke sind zueinander kongruent, wenn sie in einer Seite und den beiden anliegenden Winkeln übereinstimmen (Bild 4).
,
also ist auch .
-
Kongruenzsatz wsw
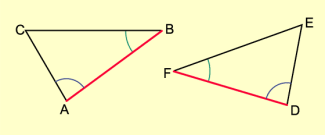
Kongruenzsatz SsW
Zwei Dreiecke sind kongruent, wenn sie in zwei Seiten und dem der größeren Seite gegenüberliegenden Winkel übereinstimmen (Bild 5).
Es sind .
Da jeweils der größeren Seite gegenüberliegen, ist
also auch .
-
Kongruenzsatz SsW
Die Beispiele im Bild 6 zeigen, warum der gegebene Winkel der größeren Seite gegenüberliegen muss.
Solange die dem gegebenen Winkel gegenüberliegende Seite a kürzer als die andere ist, gibt es entweder gar keinen , einen relativ ungenauen oder zwei Schnittpunkte mit dem freien Schenkel. Erst wenn der Radius des Kreisbogens a größer als die zweite Seite wird , gibt es mit Sicherheit nur genau einen Schnittpunkt.
-
Fälle für SsW