Zentrische Streckung
Die zentrische Streckung ist eine Abbildung. Durch eine zentrische Streckung mit dem Streckungszentrum Z und dem Streckungsfaktor (Ähnlichkeitsfaktor) k wird eine Figur F in eine ähnliche überführt. Das Streckungszentrum Z ist dabei Fixpunkt, und jede Gerade durch Z ist eine Fixgerade der Abbildung.
Die zentrische Streckung ist eine Abbildung. Durch eine zentrische Streckung mit dem Streckungszentrum Z und dem Streckungsfaktor (Ähnlichkeitsfaktor) k wird eine Figur F in eine ähnliche überführt (Bild 1). Das Streckungszentrum Z ist dabei Fixpunkt, und jede Gerade durch Z ist eine Fixgerade der Abbildung.
Die zentrische Streckung einer Figur ist durch die Angabe von Z und k bereits eindeutig bestimmt, da der Bildpunkt auf dem Strahl von Z durch P liegen muss.
-
Zentrische Streckung eines Dreiecks
Ist k = 1, so handelt es sich um eine identische Abbildung.
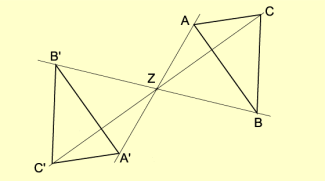
Ist k = – 1, so „fällt“ die Figur ohne Streckenlängenveränderung auf die andere Seite von Z. Es handelt sich um eine Punktspiegelung (Bild 2).
Ist , so wird die Figur vergrößert; k wird dann auch Streckfaktor genannt.
Ist , so wird die Figur verklein ert; k wird dann auch Stauchfaktor genannt.
-
Zentrische Streckung mit k = – 1
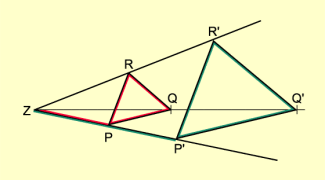
Konstruktion eines Dreiecks bei einer zentrischen Streckung (Z; k) mit k = 2 (Bild 3):
- Von einem beliebig gewählten Z aus werden die Strahlen von Z durch die Eckpunkte des Dreiecks ABC gezeichnet.
- Die Streckenlänge wird bestimmt und mit dem Streckungsfaktor k multipliziert. Man erhält die Streckenlänge , trägt diese von Z aus ab und erhält den Punkt . Analog werden die Bildpunkte und konstruiert.
- Die Bildpunkte werden in der ursprünglichen Reihenfolge miteinander verbunden.
-
Zentrische Streckung mit k = 2
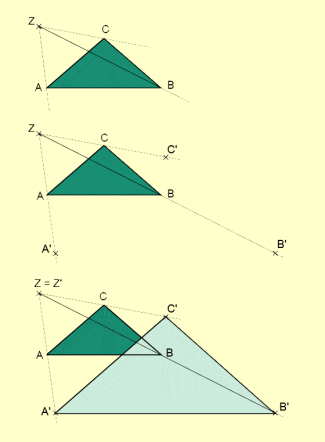
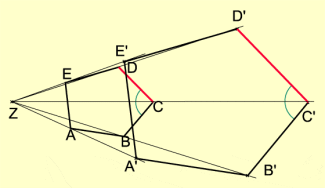
Bei jeder zentrischen Streckung gelten die folgenden Eigenschaften (Bild 4):
- Das Bild einer Gerade ist wieder eine Gerade.
- Zwei zueinander parallele Geraden besitzen als Bild wieder zueinander parallele Geraden.
- Das Bild einer Strecke ist eine zu ihr parallele Strecke.
- Je zwei Streckenlängen bilden die gleichen Verhältnisse wie ihre Bildstreckenlängen.
- Original- und Bildwinkel sind gleich groß.
- Das Bild eines n-Ecks ist wieder ein n-Eck.
Eine zentrische Streckung kann auch als maßstäbliche Vergrößerung oder Verkleinerung eines Originals bezeichnet werden. Der Streckungsfaktor k wird dann Maßstab genannt. Der Maßstab k gibt das Verhältnis der Bildstreckenlänge zur Originalstreckenlänge an.
Beispiel:
Die Hardenbergstraße in Berlin ist auf einer Karte mit dem Maßstab 1 : 15000 etwa 7 cm lang. Da die Karte eine maßstäbliche Verkleinerung darstellt, ist die Hardenbergstraße in der Wirklichkeit 15000-mal länger als auf der Karte:
Die Hardenbergstraße ist (im Original) etwa 1 km lang.
-
Eigenschaften zentrischer Streckungen
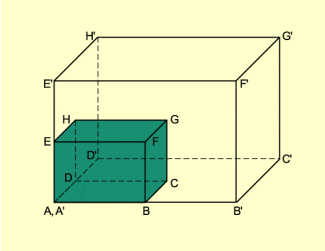
Beim Vergrößern und Verkleinern ändern sich neben den Streckenlängen auch die Flächeninhalte von Figuren. Bei Körpern wird neben dem Oberflächeninhalt auch das Volumen verändert.
Beim Vergrößern bzw. Verkleinern einer Figur mit dem Maßstab k bilden die Flächeninhalte das Verhältnis:
Beim Vergrößern bzw. Verkleinern eines Körpers mit dem Maßstab k bilden die Volumina das Verhältnis (Bild 5):
-
Vergrößerung eines Quaders mit k = 2