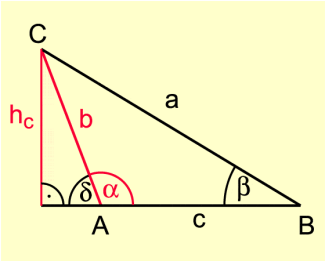
Sinussatz
Der Sinussatz verbindet gegenüberliegende Größen (Seiten und Winkel) im allgemeinen Dreieck. Sind zwei einander gegenüberliegende Größen gegeben, so kann zu einer dritten die gegenüberliegende Größe berechnet werden.
Der Sinussatz verbindet gegenüberliegende Größen (Seiten und Winkel) im allgemeinen Dreieck. Sind zwei einander gegenüberliegende Größen gegeben, so kann zu einer dritten die gegenüberliegende Größe berechnet werden. Der Sinussatz gehört neben dem Kosinussatz zu den wichtigsten Sätzen der Trigonometrie.
In jedem Dreieck verhalten sich die Längen zweier Seiten wie die
Sinuswerte der gegenüberliegenden Winkel:
a : b : c = sin : sin : sin oder
-
Sinussatz
Beweis
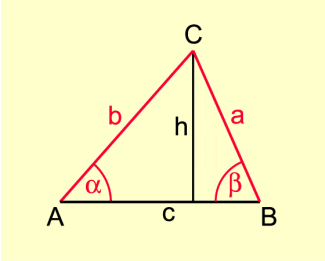
1. Fall (spitzwinkliges Dreieck, Bild 2):
Es gilt:
Daraus folgt:
a · sin = b · sin bzw. a : b = sin : sin
-
Sinussatz im spitzwinkligen Dreieck
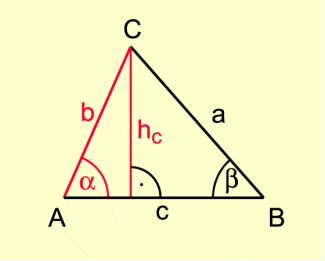
2. Fall (rechtwinkliges Dreieck, Bild 3):
Es gilt:
= a · sin und = b
Da
Daraus folgt:
a · sin = b · sin bzw. a : b = sin : sin
-
Sinussatz im rechtwinkligen Dreieck
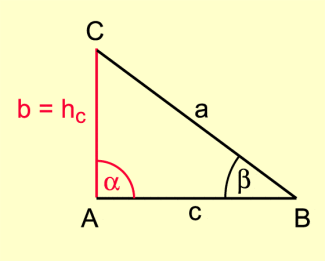
3. Fall (stumpfwinkliges Dreieck, Bild 4):
Es gilt:
sin = sin (180° - ) = sin = : b und sin = : a
Daraus folgt: bzw. a : b = sin : sin
-
Sinussatz im stumpfwinkligen Dreieck