Kugelvolumen nach Archimedes

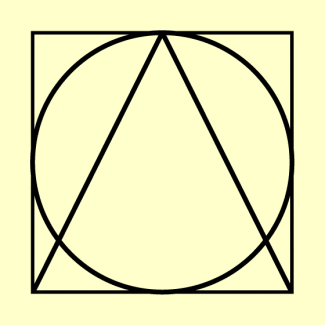
Die Herleitung der Formel zur Berechnung des Volumens einer Kugel ist eine der größten mathematischen Leistungen von ARCHIMEDES. Auf seinen Wunsch hin wurde auf seinem Grab ein Schnitt durch eine Kugel, einen Kegel und einen Zylinder eingemeißelt. Durch die Kenntnis dieser Inschrift konnte sein Grab im Jahre 75 auf einem Friedhof in Sizilien wiederentdeckt werden.

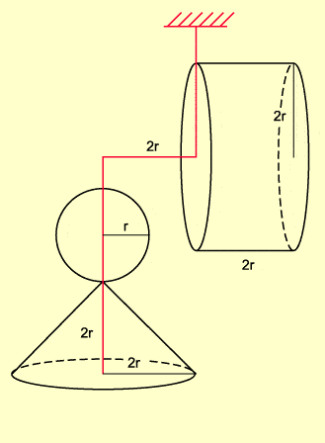
ARCHIMEDES fand die Formel für das Volumen einer Kugel durch physikalische Überlegungen. Er hängte (wahrscheinlich nur in Gedanken) eine Kugel mit dem Radius r, einen Kegel mit dem Radius 2r und der Höhe 2r sowie einen Zylinder mit dem Radius 2r und der Höhe 2r alle aus dem gleichen Material wie in Bild 3 dargestellt drehbar auf. Durch Berechnung der Drehmomente konnte er zeigen, dass sich die Anordnung im Gleichgewicht befindet.

Dann gilt nach dem Hebelgesetz folgende Beziehung zwischen den Massen der Körper und den Abständen zum Massenmittelpunkt:
$\begin{array}{l}{m}_{Kugel}\cdot 2r+m_{Kegel}\cdot 2r=m_{Zylinder}\cdot r,\\ also2\cdot m_{Kugel}+2\cdot m_{Kegel}=m_{Zylinder}\end{array}$
Da die Dichten der Körper gleich sind und die Formeln für das Kegel- und Zylindervolumen bekannt waren, konnte ARCHIMEDES daraus die Formel für das Kugelvolumen herleiten:

$\begin{array}{l}2V_{Kugel}=V_{Zylinder}-2V_{Kegel}=\pi {\left(2r\right)}^2\cdot 2r-2\cdot \frac{1}{3}\pi {\left(2r\right)}^2\cdot 2r=\frac{8}{3}\pi r^3,\\ also{V}_{Kugel}=\frac{4}{3}\pi r^3\end{array}$